1. 核力#
原子核という有限量子多体系は核子間に働く相互作用である核力の複雑さに起因して非常にrichな様相を見せる系である。 中性子過剰核(陽子過剰核)などのいわゆる不安定核は、我々の身の回りの物質を構成する安定核とは全く異なる性質を示すことも多い。 顕著なもので言うと、魔法数の破れや反転の島、ハロー核といって少数の核子が周囲に広がり弱束縛する核などがある。
こうした原子核の性質は、核子間の相互作用の複雑さに起因するものであり、核力を理解することは当然原子核の理解につながる。 しかし、核力は非常に複雑なものであり、その理解は容易ではない。
この章では、核力の基本的性質や、現代の構造・反応理論における標準的なインプットであるカイラル有効場理論に基づく核力ポテンシャルの概要を述べる。
1.1. 核力の基本的性質#
核力の持つ特徴的な振る舞いとしては、
近距離で強い斥力を持つ
1fm程度の距離ではメソン交換による引力が働く
2-3fmを超えると殆ど力が到達しない
3体系以上になると、2体系の積み重ねで説明できない3体力が働く
といった点が挙げられる。
N. Ishii, S. Aoki, and T. Hatsuda Phys. Rev. Lett. 99, 022001 (2007) の論文から、図を引用する
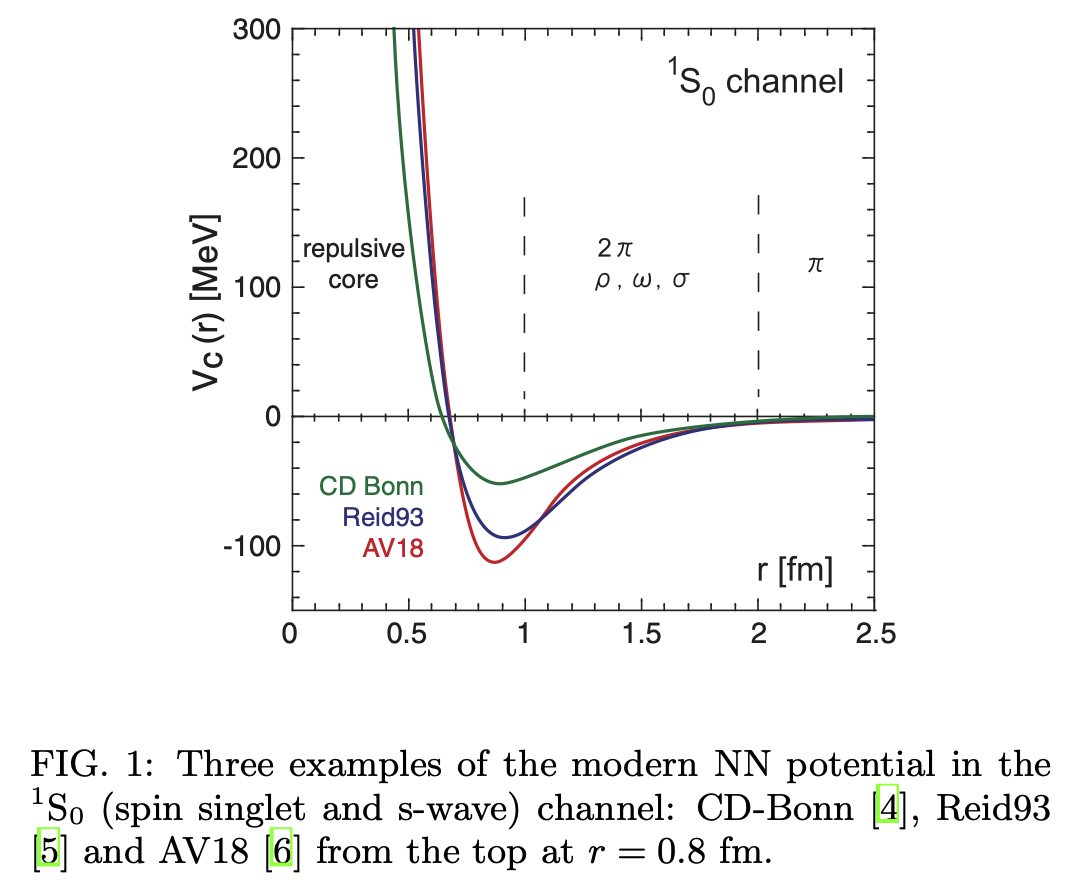
これは、核力の\(^1S_0\)成分について、距離\(r\)の関数として現実的核力(CD-Bonn, Reid93, AV18)をプロットしたものである。 斥力芯や中間子交換による引力の寄与が見て取れる。※核力のチャンネルや現実的核力については後述する。
1.1.1. アイソスピン#
proton |
neutron |
|
|---|---|---|
電荷 |
e |
0 |
質量 (MeV) |
938.272 |
939.550 |
スピン |
1/2 |
1/2 |
半減期 |
\(>10^{34}\) yr |
887 s |
組成 |
uud |
udd |
陽子と中性子の質量はほぼ同じであるため、同一の粒子(核子)の異なる荷電状態とみなして扱う事が多い。
ハイゼンベルクは電子のスピンに類似した核子の内部自由度を導入し、それをアイソスピンと呼んだ。
もちろんこれは、核子の内部構造であったり、電磁相互作用/弱い相互作用などの影響を無視した近似であるが、 核子間の相互作用を記述する上で、アイソスピンを導入することは非常に有効であることが経験的に分かっている。
それぞれの相互作用を分類する際には、proton-proton: pp, neutron-neutron: nn, proton-neutron: pnなどと表記することにする。
pn系は、スピンの場合と同じく(合成)アイソスピンを用いて
\(I=1\)成分 → \(\frac{1}{\sqrt{2}} (|n\rangle|p\rangle + |p\rangle|n\rangle)\)
\(I=0\)成分 → \(\frac{1}{\sqrt{2}} (|n\rangle|p\rangle - |p\rangle|n\rangle)\)
と分類することができる。
1.1.2. 核力の持つ基本的対称性#
核力には、基本的性質として以下の対称性(不変性)がある。 核子の番号をそれぞれ1,2とすると、以下のように対称性・不変性から依存性(一般形)を限定することができる:
核子の座標の交換に対する対称性: \(V(1,2) = V(2,1)\)
並進対称性: 核子間の相対座標\(\boldsymbol{r}\equiv \boldsymbol{r}_1-\boldsymbol{r}_2\)のみに依存する
ガリレイ不変性: 核子間の相対運動量\(\boldsymbol{p}\equiv \boldsymbol{p}_1-\boldsymbol{p}_2\)のみに依存する
空間反転不変性: 座標とスピンのflipに対して不変
時間反転不変性: 運動量とスピンのflipに対して不変
回転不変性: 各項は既約テンソルの意味でスカラーになる
アイソスピン空間の回転不変性: \(I=1\)(3重項)に属する相互作用はpp,nn,pnで同じになる(合成のアイソスピンのみに依存)。
では、それぞれの項の強さはどのように決定すればよいだろうか?
格子QCD計算によって、核力を含むハドロン間相互作用をQCDに基づいて記述する試みとして、 HAL QCD法による研究は特筆すべき成果を挙げている。 先程の図でも引用した論文、N. Ishii, S. Aoki, and T. Hatsuda Phys. Rev. Lett. 99, 022001 (2007) では、核力の近距離における斥力芯や、中-長距離における引力的な振る舞いをQCDから第一原理的に示すことに成功している、 マイルストーン的な研究である。 一方で、後述の3体力を含む核力の様々なチャネルを含む核力の様々な寄与をQCDから定量的に再現することは依然として困難である。
1.1.3. 現実的核力#
主に90年代以降、現実的核力と呼ばれる核子間相互作用が提案されてきた。
これは、大雑把に言えば、核子間の相互作用の基本的な性質を反映した項を考え、
NN散乱などの反応データ(3000とか4000以上)をもとに、それらの項のパラメータを調整することで構築されたものである。
代表的なものとしては、Argonne (\(v_{18}\))、
CD-Bonn、Nijmegenなどがある。
現実的核力の構築に伴い、それらを直接のインプットとする第一原理計算の研究も盛んになった。 特に重要な仕事を2つほど紹介しておく。
Quantum Monte Carlo calculations of A=8 nuclei, R. B. Wiringa et al., Phys. Rev. C 62, 014001 (2000)
この仕事では、Argonne v18(+Urbana IX 3体力)をインプットとして、軽い核のVMC&GFMC計算を行っている。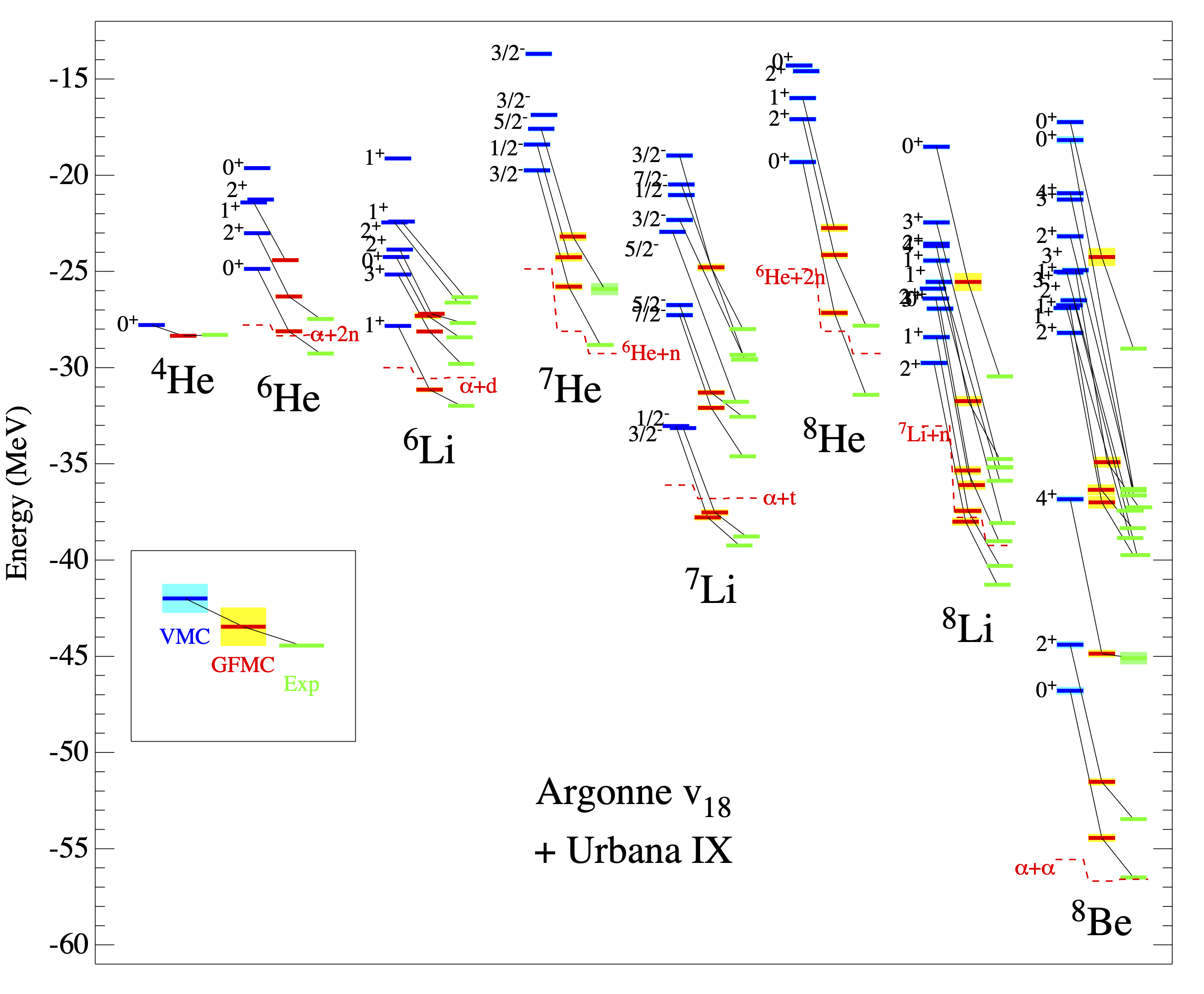
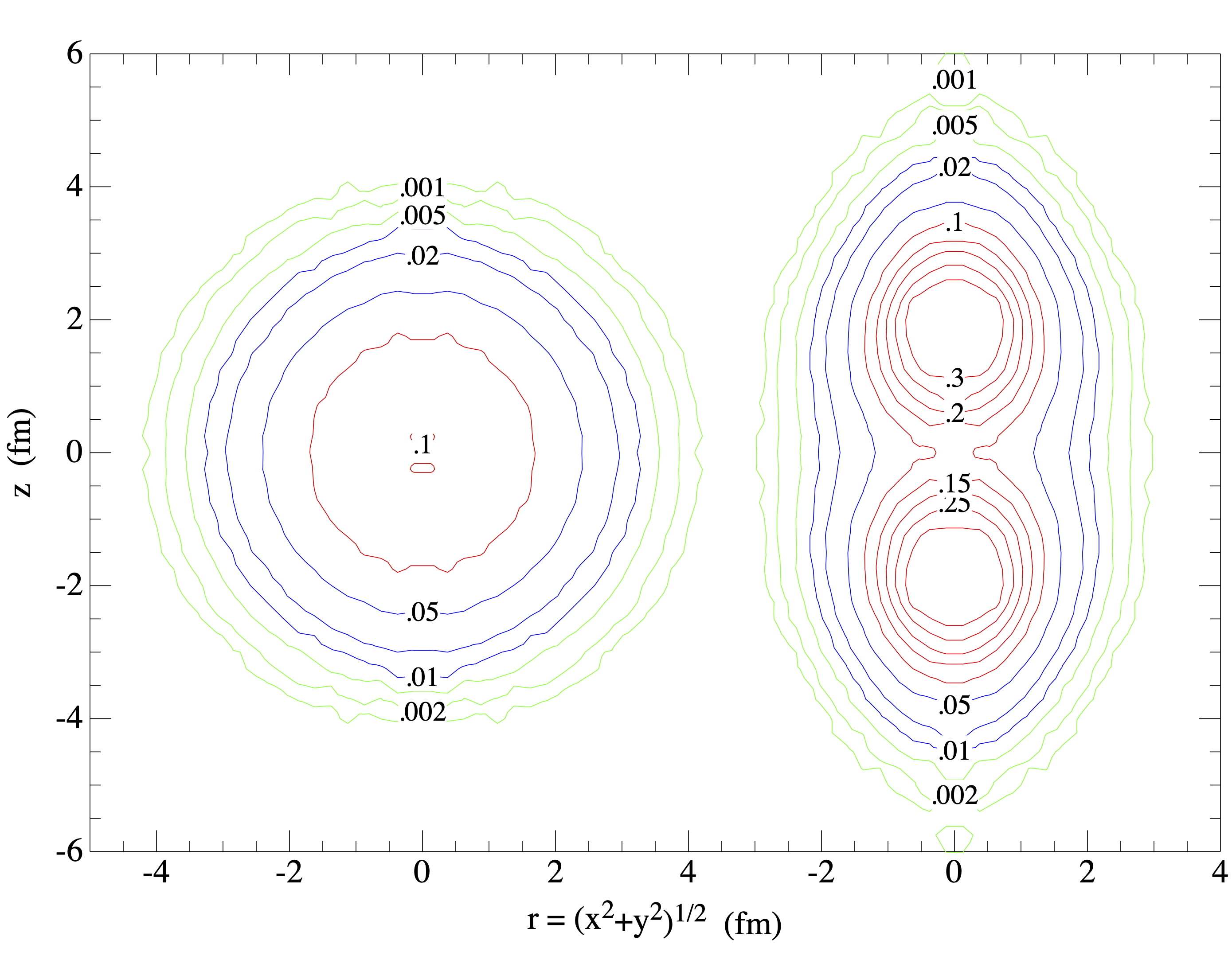
図左側にA=4-8の核の基底状態・及び励起状態のスペクトルを示している。 基底状態エネルギーの系統的なズレはあるものの、核力をインプットとする計算が、軽い核のスペクトルをよく再現していることがわかる。
図右側には \({}^{8}\mathrm{Be}\) の基底状態の密度分布が示されている。 \({}^{8}\mathrm{Be}\) は、すぐに2つの\(\alpha\)粒子に崩壊する不安定核で、 基底状態においてtwo-\(\alpha\)クラスターの成分を持つと考えられる。
左側のプロットが実験室系での密度分布、右側が物体固定座標系での密度分布である。 クラスター構造を仮定せずに初めて核力から \(2\alpha\) の成分を持つことを示したマイルストーン的な仕事である。
Large-basis ab initio no-core shell model and its application to 12C, P. Navrátil et al., Phys. Rev. C 62, 054311 (2000)
この仕事では、CD-BonnやArgonne v8'をインプットとして、軽い核のno-core shell model(NCSM)計算を行っている。
炭素12の基底状態エネルギー-92.162MeVに対して、当時扱える最も大きい基底空間での計算で-88.518(CD-Bonn), -87.675(AV8')と そこそこの精度の記述を与えている。また、励起状態についても、Hoyle状態(Ex.=7.65 MeV)のようなエキゾチックな状態を除いて、 かなりの精度で記述できていることが伺える。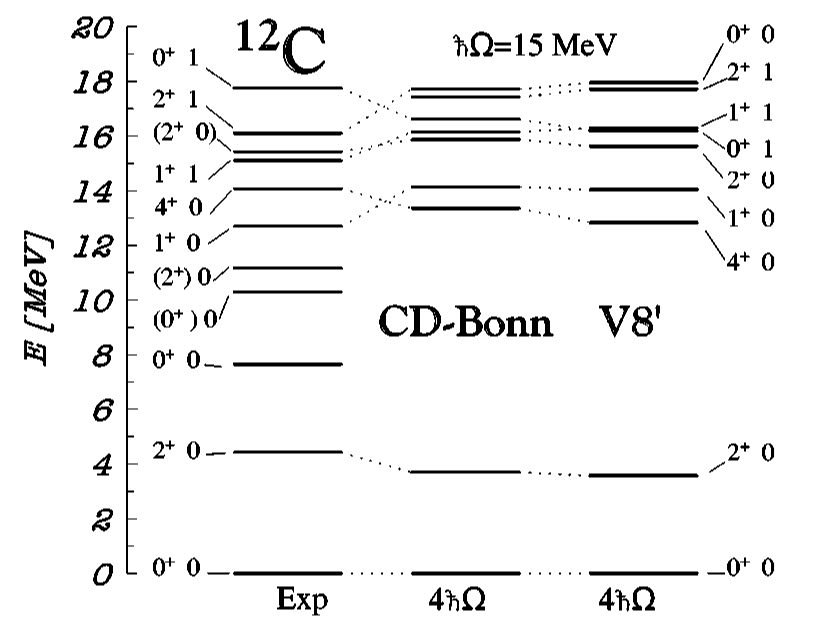
1.1.4. カイラル有効場の理論#
2000年代以降は、カイラル有効場理論(Chiral EFT)に基づく核力が提案され、 とくに2010年以降、微視的な核構造・核反応計算の標準的なインプットとして用いられるようになっている。
カイラル有効場理論は、QCDの低エネルギー有効理論であり、有効ラグランジアンを出発点に、 2体力・3体力(より高次の多体力)を系統的に導出することができる。 どの自由度をあらわに扱い、カイラル摂動論を考えるかによって、様々なバリエーションはあるが、 以下ではとくに、核子と核力を媒介するパイオンのみを顕な自由度として扱うものを指して、カイラル有効場理論と呼ぶことにする。
Chiral EFTに基づく核力の整理を示す図を下に示した(出典→Phys. Rep. 503, 1 (2011))。
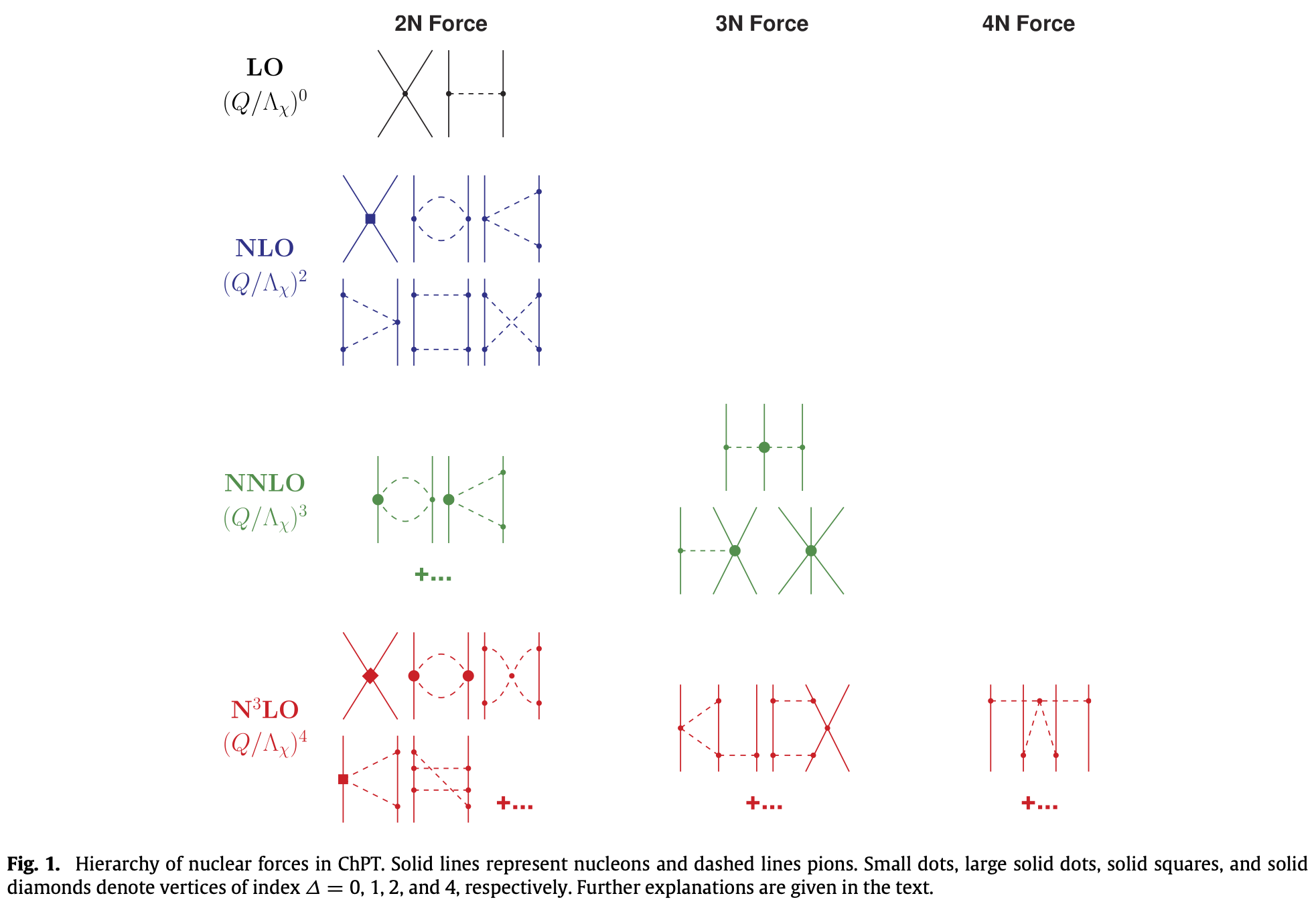
それぞれの寄与の順序は、power-countingによって決まる。 例えば2体力の主要な寄与(leading order; LO)に着目すると、2つのダイアグラムがあることが見てとれる。 このうち、湯川の中間子理論における核力, OPEP(One-pion exchange potential)の寄与が 2つめのダイアグラムに対応する。 1つ目の項(コンタクト項)は、pion以外の中間子の交換による相互作用などを表している。 核子とパイオンのみを顕な自由度として扱う場合、それ以外の自由度の寄与はこのコンタクト項のように、 vertex部分に吸収されることになる。 それぞれのvertexには、低エネルギー係数(LEC)と呼ばれるパラメータが現れ、 核力の場合は、核子-核子や核子-パイオンの散乱データをもとに、 これらのパラメータを調整することで核力を構築することができる。 散乱データをもとに核力を構築する考え方自体は、現実的核力と呼ばれていた核力と同様である。
また、3体力については、NNLOに3つの寄与が現れている。中でもひときわ重要なのが、 TPE(Two-pion exchange)と呼ばれる項であり、藤田-宮沢型3体力と呼ばれる3体力の主要な寄与に対応するものである。
筆者はカイラル摂動論については全くの素人以下なので、一般論はこの辺りに留めて、以下ではユーザーの立場からもう少し整理を行う。
カイラル有効場の理論に基づく核力ポテンシャルには(派生した相互作用もあるが)代表的には2つの系統があり、幾つか呼ばれ方が異なることもある。
Idaho系 Ruprecht Machleidtらを中心としたグループが提案したもの。
D.R. Entem and R. Machleidt, Phys. Rev. C 68, 041001 (2003). が有名。N3LOまでのNN核力を含み、Entem-Machleidt型と呼ばれたり、EMなど略される。 カットオフが500MeVの通称EM500が、これまでに最も多く構造・反応計算で用いられてきた。
N4LOのTPEの寄与はEntem,Kaiser, Machleidt, Nosykらによる論文Phys. Rev. C 91, 014002 (2015)によって与えれ、その後、Contact項も含めてN4LOまでのLECsを散乱データにfitした EMNと呼ばれる系統が提案され、2017年以降のab initio計算の標準的なインプットとなっている→D. R. Entem, R. Machleidt, and Y. Nosyk Phys. Rev. C 96, 024004 (2017)その他、詳細はレビュー論文に譲る → Phys. Rep. 503, 1 (2011) Front. in Phys. 8 (2020) 57
Jülich系 Bochum-Jülichグループが提案したもの。当初は Evgeny Epelbaum, Ulf-G. Meissner, Walter Gloeckleらの頭文字を取ってEGMなどとも呼ばれていたが、 近年では、JülichポテンシャルやLENPICポテンシャル(LENPIC collaborationから)などと呼ぶことが多い印象。
レビュー論文 → Rev. Mod. Phys. 81, 1773 (2009), Front. in Phys. 8 (2020) 98
この他、中重核の束縛エネルギーと核半径を再現するようにfitされた相互作用(例: NNLOsat)や Full-CI用に最適化された相互作用(例: JISP16, Daejeon16)なども提案されひろく用いられているが、ここでは割愛する。
以降では、主にIdaho系の2体相互作用を用いることにする。
1.1.5. 3体力#
核子間相互作用は、核子が複合粒子であることに由来して、2体力だけでなく3体力(および高次の多体力)が働く。
3体力の重要性は様々な系で指摘されてきたが、とりわけ以下の2点からその重要性が強調されることも多い。
有限核の束縛エネルギーの説明
核子-核子などの散乱データを精度良く記述する2体力を用いて第一原理計算を行うと、 \({}^{4}\mathrm{He}\)などの軽い核の束縛エネルギーは実験値を過小評価し、 \({}^{16}\mathrm{O}\)や\({}^{40}\mathrm{Ca}\)などの中重核をはじめ、重い核の束縛エネルギーの実験値を過大評価することが知られている。 これは、2体力だけでは核子間の相互作用を十分に記述できていないことを示唆しており、 軽い核では引力的、ある一定の質量数以降の重い核では斥力的な3体力が働いていることが示唆される。無限系
対称核物質の飽和性※や、中性子星(とくに太陽質量の2倍を超えるような重い中性子星)の質量半径関係などから、 斥力的な3体力が不可欠であることが示唆される。
※ エネルギーvs密度の関数は最小点( \(\rho \sim 0.16\) fm \(^{-3}\) )を持ち、密度の飽和性とも呼ばれる。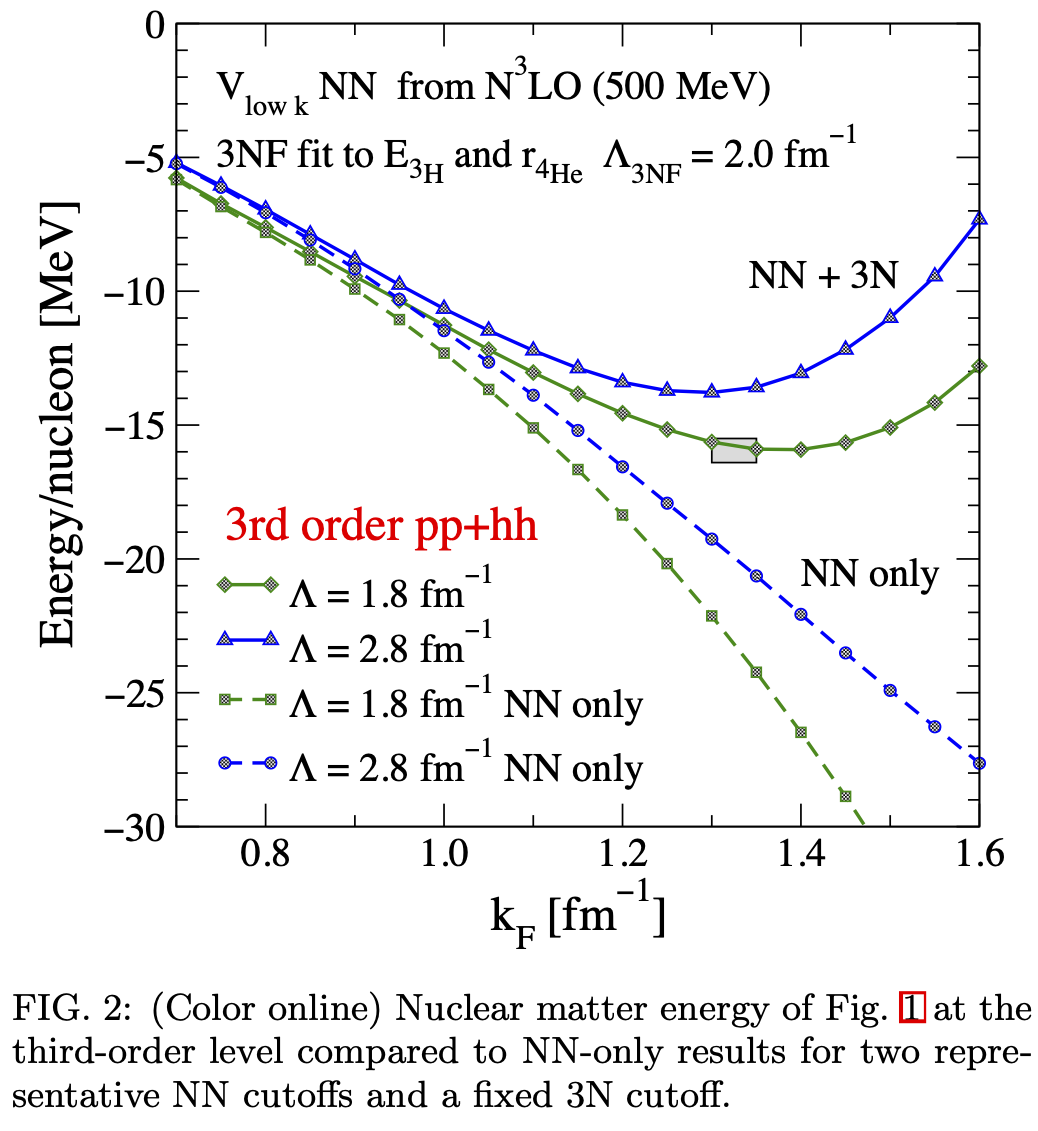
図は、K. Hebeler et al., Phys. Rev. C 83, 031301(R) (2011)の図2、対称核物質の核子あたりのエネルギー(vs Fermi momentum)を示したものである。 カイラル相互作用の2体力だけでは、飽和密度を再現出来ないことが分かる。
3体力の難しさと面白さは、講義の時間(や筆者の能力)でカバーしきれるものではないので、資料では簡単な言及に留めておく。
少数系から無限系に至るまでをカバーしたレビュー論文として、以下のものを挙げておく:
K. Hebeler, Phys. Repo. 890, 1 (2021)
1.2. 核力の表示: momentum space#
核力の表示は様々あるが、以下では、最も一般的な表示の一つである、momentum spaceでの表示を用いる。
この資料では、重心系(2核子の重心運動を取り除いた相対運動量)で常に記述することを最初に断っておく。 つまり、核子1の運動量を\(\vec{p}\)とすると、核子2の運動量は\(-\vec{p}\)となる座標系を考える。
この2核子対が互いに相互作用を及ぼし合うとき、散乱の始状態・終状態の運動量をそれぞれ\(\vec{p}\)、\(\vec{p}'\)とし、 平均運動量を\(\vec{k} = \frac{1}{2}(\vec{p}+\vec{p}')\)、運動量移行を\(\vec{q}=\vec{p}-\vec{p}'\)とする。 このとき相互作用は
といった一般的な形で書くことができる。\(V\)や\(W\)はそれぞれ、運動量やスピンへの依存性で寄与を整理するもので、 \(C\) (central), \(S\) (spin), \(LS\) (spin-orbit), \(T\) (tensor), \(\sigma L\) (spin-spin-orbit)などと分類され、それぞれが \( k\equiv | \vec{k} | \) や \(q\equiv | \vec{q} |\) の関数となる。 例えばMachleidtらのレビュー論文Phys. Rep. 503, 1 (2011)をみると、カイラル摂動論に基づいてこうした各項の振幅を計算する方法が示されている事がわかる。
例を幾つか挙げよう:
OPEP(One-pion exchange potential@LO)
\[ V(p,p') = - \frac{g_A^2}{4 f_\pi^2} \vec{\tau}_1 \cdot \vec{\tau}_2 \frac{\sigma_1 \cdot \vec{q} \sigma_2 \cdot \vec{q}}{q^2 + m_\pi^2 } \]
NLOにおける\(W_C\)項 EM reviewの(4.9)式:
\[\begin{split} \begin{align} W_C(p,p') & = - \frac{L(q)}{384 \pi^2 f^4_\pi} \left[ 4 m_\pi^2 (5g^4_A -4g_A^2 -1) + q^2 (23g^4_A - 10g^2_A - 1) + \frac{48g^4_Am^4_\pi}{w^2} \right] \nonumber \\ w & = \sqrt{q^2 + 4m^2_\pi} \nonumber \\ L(q) & = \frac{w}{q}\ln \left(\frac{w+q}{2m_\pi}\right) \nonumber \end{align} \end{split}\]
1.2.1. partial-wave momentum space: \(\langle p';L'S'J'T_z |V|p;LSJT_z\rangle\)#
さて、上の一般系の核力を、いわゆるpartial-wave decompositionした形で書くことを考える。
つまり、核力ポテンシャルを合成の軌道角運動量やスピンなどの量子数で分類することを考える。
重水素の束縛エネルギーの記述であるとか、散乱断面積の解釈などには、こちらの表示が有用である。
momentum spaceの相互作用を、2核子の合成軌道角運動量\(L\)、合成スピン\(S\)、合成角運動量\(J\), \(T_z\) に応じて、\(^1S_0\), \(^3S_1\), ... といった形で表示することを考える。
この際、上で導入した\(V, W\)の各項について、各成分\(\alpha=\{C,S,LS,T,\sigma L\}\)の係数の 線形結合でもって、\(V(^1S_0) = \sum_{\alpha} C_{\alpha} V_{\alpha}\)などとして チャンネルごとのポテンシャルを表現することができる。より詳細にはMachleidtらのレビュー論文を参照のこと。
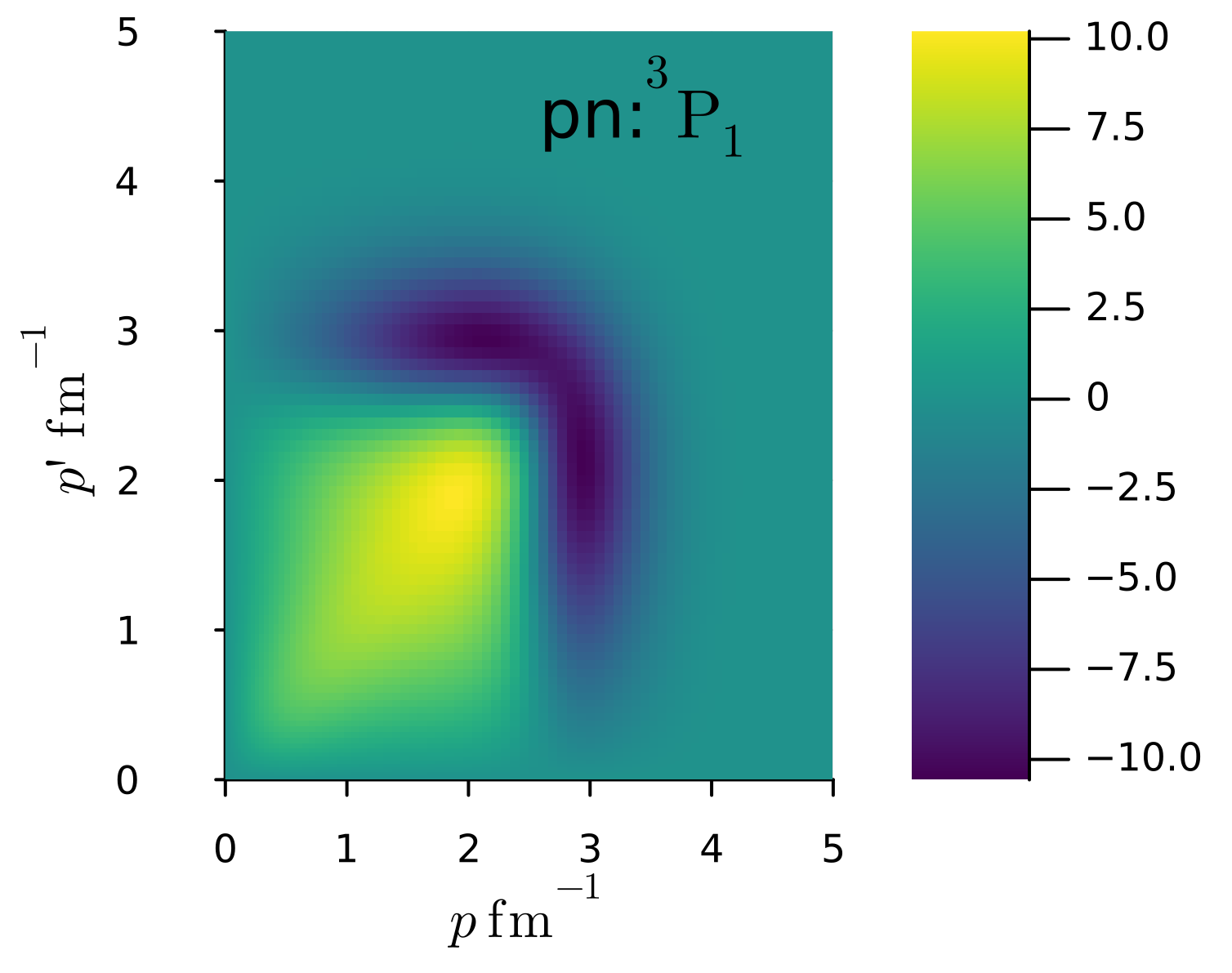
これによって、合成の軌道角運動量など量子数の組\(\{L,S,J,T_z\}\)ごとに\(p-p'\)平面で核力ポテンシャルを表示することができる。
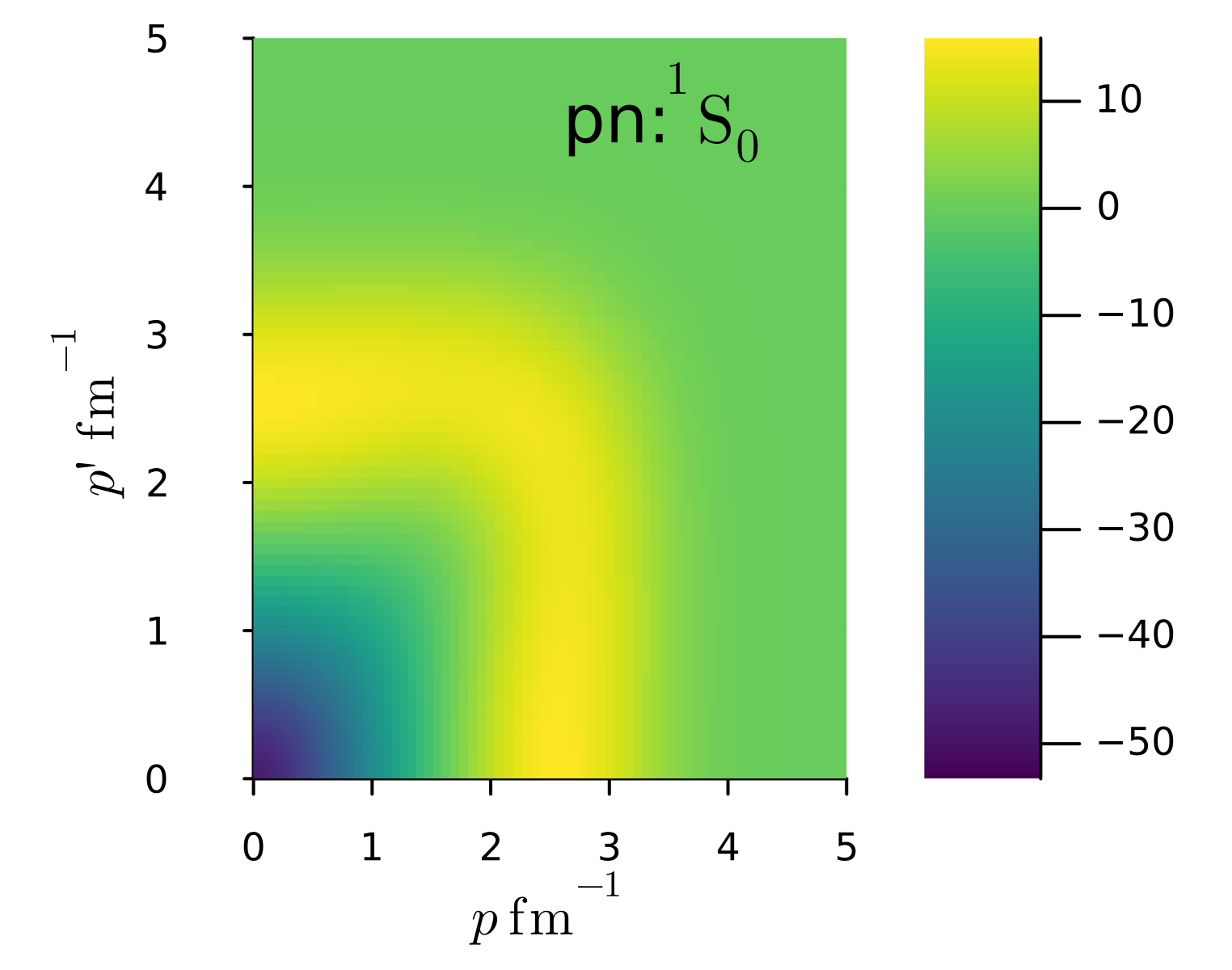
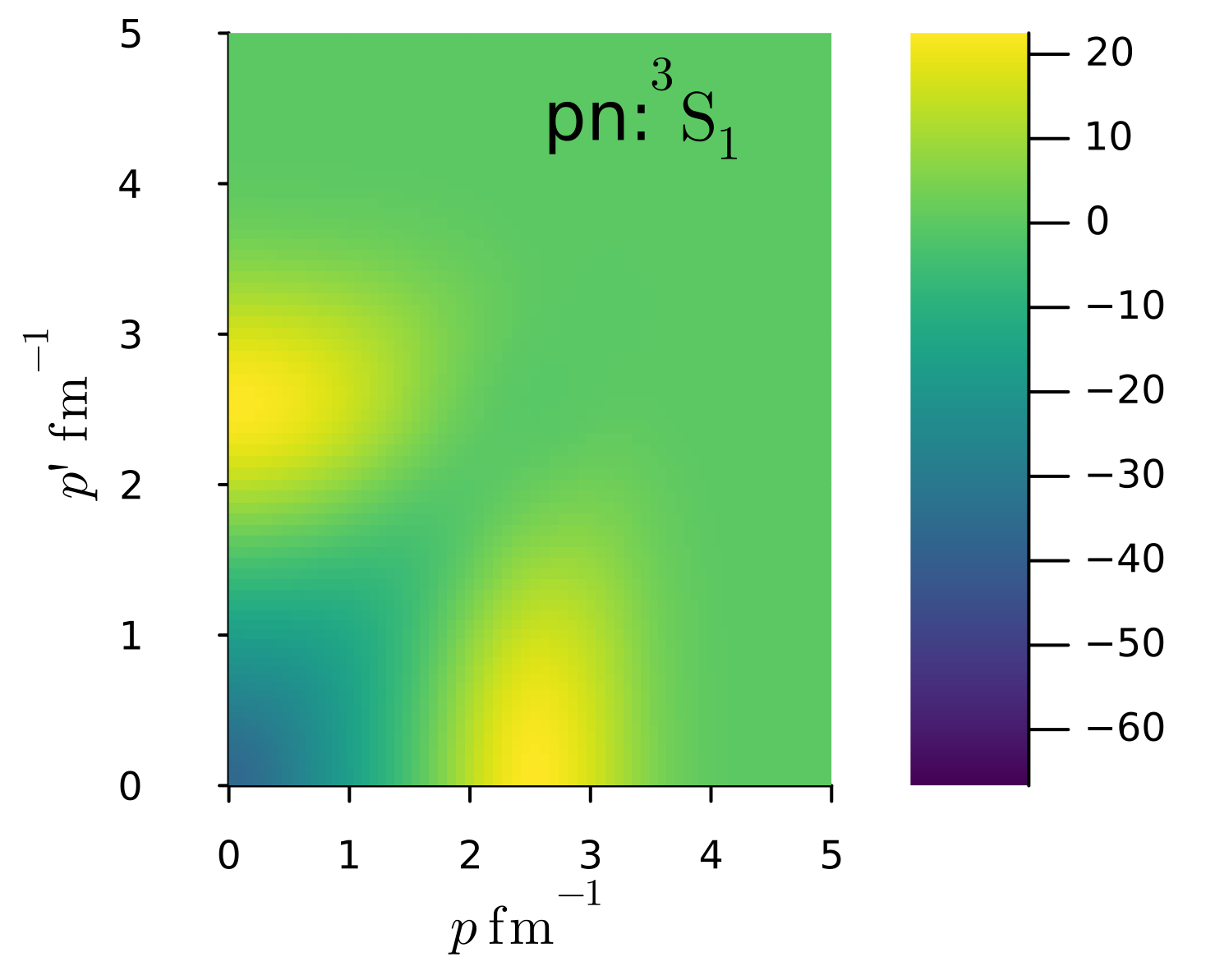
下に、proton-neutron間2体力の\(^1S_0\), \(^3S_1\), \(^3P_1\)の各成分を示した。
1.2.2. single-particle space (single-particle Harmoic oscillator basis)#
実際の核構造計算手法では、核力を\(\{n,\ell,j,t_z\}\)の足を持った調和振動子基底(Harmonic oscillator basis)で展開して使う場合が多い。 これは、閉殻芯に対応する占有軌道や、非占有軌道をバレンス空間とそれ以外に分類しやすく、 conventionalな殻模型計算のように分かりやすい解釈を与えてくれる、という理由もあるように思う。
核力ポテンシャルを、jj-couplingの軌道に対応する\(\{n,\ell,j,t_z\}\)の足を持った基底で展開することを考える。
ここで、\(a,b,c,d\)は、\(\{n, \ell, j, t_z\}\)の量子数に対応するラベルである。
上のpartial-wave momentum spaceでの表示を、single-particle spaceでの表示に変換する際、 通常、2つのステップを踏むことになる。 1つが、(2体)HO基底での表示に変換すること、もう1つが、(1体)HO基底での表示に変換することである。
一般的なmomentum-spaceの行列要素\(\langle p' \alpha | V | p \alpha \rangle\)を、
調和振動子基底の行列要素に変換する
ここで、\(\alpha\)は上でも登場した\(L, S, J, T_z\)の組み合わせなどをまとめて表すラベルである。
\(b\)はoscillator parameterで、\(b^{-1} = \sqrt{m\Omega}\), \(L^k_n\)は一般化Laguerre多項式である。
two-body HO basisでは、「2核子の相対運動を調和振動子基底で展開しただけの数学的処理」と解釈すると良いかもしれない。 Jacobi座標(運動量)を導入することで、この操作は自然に3体力に拡張することができる。あるいは、重心運動を陽に扱う場合にも、\(N\)は\(n_\mathrm{rel},N_\mathrm{CM}\)、\(L\)は\(\ell_\mathrm{rel},L_\mathrm{CM}\)など重心・相対運動の量子数を区別して別々に計算する必要がある。
(two-bodyの)HO基底をsingle-particle HOに変換する操作は、有名なTalmi-Moshinsky変換である。 CM&relativeの2体調和振動子の量子数をそれぞれ\(N,L\), \(n, \ell\)とすると、 single-particle HOへの変換は以下のような形で与えられる:
\(\langle n N [(\ell L) \Lambda S]J | n_a n_b [(\ell_a \ell_b)\Lambda (\tfrac{1}{2}\tfrac{1}{2})S] J \rangle_{d=1}\)部分が、いわゆるMoshinsky bracketやHO bracketなどと呼ばれるものであり、実装においては、G.P. Kamuntavičius et al., Nucl. Phys. A 695, 1 (2001)が最もよく引用されている。
single-particle HOは、jj-couplingの意味での調和振動子なので、物理的な解釈がしやすい。
1.3. 核力のソフト化#
核力は、先に示したように、(チャンネルによるが)短距離で非常に強い斥力を示す相互作用であるため、散乱データをfitして得た現実的核力/カイラル核力をそのまま 構造計算のインプットに使うと、発散してまともな計算ができなかったり、計算結果が安定しなかったりする。
そこで用いられるのが核力のソフト化と呼ばれる操作である。 対比として、ソフト化を施す前の相互作用をbareな核力(bareな相互作用)と呼んだりもする。 歴史的にはBrucknerの\(G\)行列や、散乱のT行列を保持するように高運動量成分をカットする\(V_\mathrm{low k}\)など関連する事項があるが、 ここではより現代的なSimilarity Renormalization Group (SRG)を用いたソフト化についてのみ紹介する。
SRGは、S.K.Bogner et. al., Phys. Rev. C 75, 061001(R) (2007)で提案された手法である。
元の相互作用と等価な(物理量を変えない)、高運動量成分(短距離成分)を取り除いた相互作用を得るため、核力のHamiltonianに対する以下のユニタリ変換(SRG変換)を考えよう:
SRG変換を変換のgenerator(生成子)である\(\eta(s)\)を導入し、フロー方程式の形で表すと
と書くことができる。\(H(s=0)\)がbareな核力に対応する。
generatorの選び方によって、核力のソフト化の程度や性質を調整することができる。
SRG変換とgeneratorの関係についての一般論としては、\(H(s)\)はgeneratorと似た構造を持つよう変換を受けることが重要である。
Wigner, White, など様々なgeneratorが提案されているが、2体力レベルではHamiltonianの(partial wave p-p'平面の意味で)対角成分を採用する事が多い。
bareなHamiltonianは、高運動量と低運動量成分をcoupleするような寄与(座標空間でいうと、近距離≒斥力芯に対応する成分)が大きく、 これが計算を困難にする原因となっているわけだが、SRG変換によって、この成分をdecoupleした有効核力を得ることができる。
ユニタリ変換の性質上、SRG変換によってHamiltonianの固有値は変化しない。 ただし、ここにはトリックがあり、SRG変換によって生成(induce)される多体力を全て考慮すれば上の主張は正しいが、 実際の多体計算においては、SRG変換によって生成される多体力を無視したり、 induced-3NFまでのみを考慮したりすることが多く、上の主張は厳密には成り立たない。
少なくとも2体のレベルで正しい操作をしているかどうかは、SRG変換の前後で、2体系の物理量(e.g. deuteronのbinding energy)が一致するかどうかを確認すればよい。実際、後で見るように、SRG変換によってdeuteronのbinding energyは変更を受けない。 また、2体力と同様に、3体力のSRG変換も提案され、実際に多体計算に用いられている。 詳細については割愛するが、R. Roth et al., Phys. Rev. C 90, 024325 (2014)のほか、Angelo Calci氏の博士論文が最も詳しい。
1.4. 相互作用ファイルの作成#
次に、NuclearToolkit.jlを用いて、カイラル核力(2体力のみ)の相互作用を計算してみよう。
NuclearToolkit.jlでは、相互作用ファイルを作成するためのインターフェースとしてmake_chiEFTint関数が用意されている。
ファイルを読んでオプションを指定する方式を採用している都合上、少々JupyterNotebook上での実行と馴染まないところがあるが、
実行ディレクトリにoptional_parameters.jlというファイルを用意してオプションを書き換えるか、
make_chiEFTint関数のoptional argumentとしてオプションを指定するファイルを与えてやればよい:
make_chiEFTint(;fn_params="path_to_your_file")
細かなオプションの指定は、Document中のこちらのページ やレポジトリ内のサンプルファイルを参照のこと。
オプションのうち、以下の議論で重要になるのが、single-particle HO基底のサイズを決める\(e_\mathrm{max}\)と、 HOのパラメータ\(\hbar\omega\)である。 \(\hbar\omega\)は、基底を構成する調和振動子のエネルギー間隔に対応する量で、 十分大きな模型空間を取れば、計算結果は\(\hbar\omega\)に依存しなくなると期待される。
以下では、デフォルト値を使って、カイラル核力(2体力のみ)の相互作用ファイルを作ってみよう.
using NuclearToolkit
make_chiEFTint()
size of dWS (jmax 9 lmax 40 e2max 8 Nnmax 20):
dtri 4.46 MB dcgm0 1.11 MB d6j_int 1.11 MB d6j_lj 0.28 MB
d9j_lsj 1.76 MB dictHOB 0.44 MB
E(2H): bare = -2.224578 srg = -2.224578 Diff.1.484e-10
true
make_chiEFTint関数を引数無しで実行すると、以下の手順
Entem MachleidtのN3LO相互作用, カットオフは\(\Lambda=500\) MeV
\(e_{\mathrm{max}}=4\)
\(\hbar\omega=20\) MeV
運動量空間においてSRGを適用しソフト化する (\(\lambda=2.0\) fm^{-1}$)
single-particle HO基底の相互作用ファイルをバイナリファイルとして書き出す。
このバイナリファイルは殻模型計算コードKSHELLやNuclearToolkit.jlで用いられる.sntフォーマットと呼ばれるものをバイナリ化したものになっている。なお、KSHELLでFull CIやvalence CI計算を行う場合は、対応するテキストファイルにする必要がある(そのためのオプションもある)。
sntファイルの詳細についてはDocument中のこの項目が参考になるが、概要だけ説明すると、single particle stateの定義(\(\{n,\ell,j,tz\}\)に対応)と、一粒子エネルギー(single particle energy, SPE)と二体行列要素(two-body matrix element, TBME)を格納したファイルになっている。
また、上の実行結果で表示されているように、momentum spaceでの相互作用を計算した後、 deuteronのbinding energyが評価されている。 実験値-2.224579を再現する結果が得られていることと、SRGによって値が変化しないことが確認できる。
1.4.1. 運動量空間におけるカイラル核力の2次元プロット#
partial-wave momentum spaceでの核力の表示で、Entem MachleidtのN3LO相互作用を作成した場合の \(^1S_0, ^3S_1\)成分(proton-neutron間力)を、2次元プロットしてみよう。 左から順に、対角部分(bare vs SRG), bare核力の二次元プロット, SRG変換後の核力の二次元プロットになっている。
\(^1S_0\)成分:
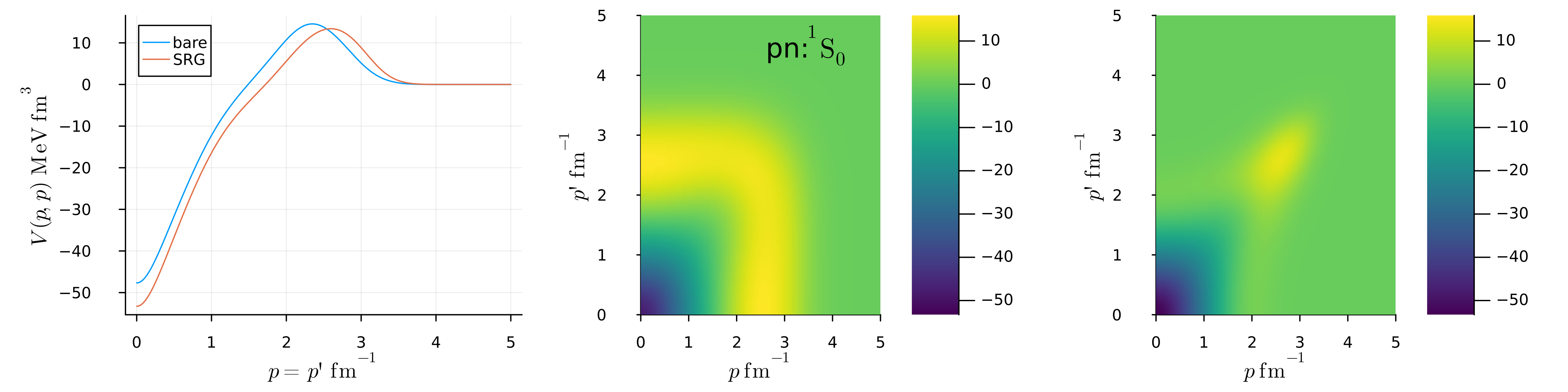
\(^3S_1\)成分:
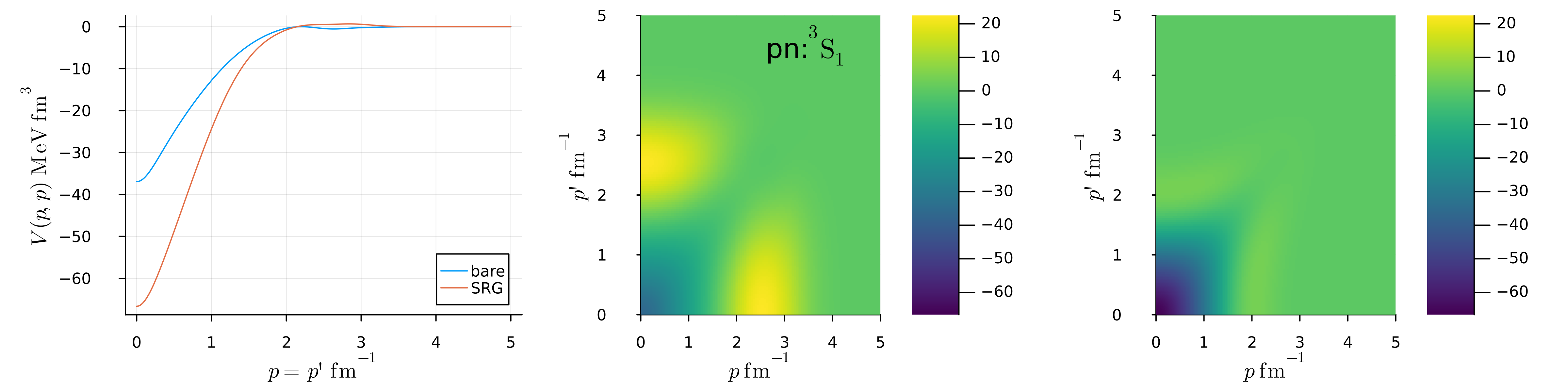
partial-waveで見た2対角力核力の成分は、どれを見ても3.5fm程度の距離で0になる。
これは、カイラル核力において、500MeVのカットオフが入っているためである。
NN力では、下記のnon-local regulatorを用いるのが一般的。
SRG変換によって、とくに非対角成分(低運動量と高運動量のカップリング)が小さくなっている傾向が見て取れる。
カイラルの相互作用は元々カットオフが入っており従来の現実的核力よりも比較的ソフトな相互作用であるが、
それでもなお、有限の模型空間で計算を行う際には、SRG変換などのソフト化を行わないと、基底状態エネルギーが発散してしまうこともある。
1.5. 3体力を含む核力計算コード#
3体力を含む核力の計算コードとして、筆者の大学院時代の先輩にあたる宮城宇志氏によるNuHamilというコードがある。
現代的な3体力もカバーしているため、興味のある方は一度目を通してみると良いだろう。
論文はこちらT. Miyagi, Eur. Phys. J. A 59, 150 (2023).
NuclearToolkit.jlでも、NuHamilが与える3体行列要素を扱えるよう拡張を行っており、v.0.4.0(2024/2/25)から利用可能となっている。
1.5.1. \(\clubsuit\) 余談: Magic interaction: EM1.8/2.0#
とくにab initio計算のコミュニティにおいて、Magicと称されるカイラル核力が知られている。
前述のmatterの計算を主に対象とするK.Hebeler et al., PRC 83, 031301(R) (2011)において、提案されたものだが、出版されしばらくして、中重核に適用すると、IM-SRG計算において、\({}^4\mathrm{He}\)から\({}^{78}\mathrm{Ni}\)領域の基底状態エネルギーと荷電半径をよく再現することがわかった。 → J. Simonis et al., Phys. Rev. C 96, 014303 (2017).
この相互作用はもともと、カイラル核力のEM500(N3LO)相互作用を、SRG変換によって\(\lambda=1.8\) \(\mathrm{fm}^{-1}\) までソフト化した2体力に、3-4体系の物理量を再現するようgenuine3体力を加えたものである。
この相互作用は、3体力のSRGなどを考えない上、2体力のSRGによりinduceされる3体力についても無視しているため、2体力と3体力のconsistentな取り扱いとは言えないものの、\({}^4\mathrm{He}\)から\({}^{78}\mathrm{Ni}\)の基底状態エネルギーと荷電半径をよく再現することが知られており、その理由が非自明なことも含めて、magicと称されている。
カットオフやinduce多体力の寄与が、genuineな3体力のfitで(意図せず)補われて、高い精度が得られていることが示唆されるが、まだまだ議論は続いている。 また、この仕事をきっかけに、中重核をよく記述する核力の条件として、対称核物質の飽和性を再現することが重要であることが示唆され、関連する研究が進められた。 2024年3月時点においても、この相互作用を劇的に超える高い精度で、\({}^4\mathrm{He}\)から\({}^{78}\mathrm{Ni}\)の基底状態エネルギーと荷電半径を再現するカイラルの相互作用は存在しない。 ab initio計算とはその性質上「真面目にやれば正しい結果が得られるだろう」と期待するものだが、この相互作用は、そのような期待を裏切るものであるともいえ、なんとも面白い相互作用である。
その後の研究により、質量と半径やnuclear matterの計算には、non-local cutoffを用いた3体力が適していることが示唆されるようになった。 これを受けて提唱された、2体力と3体力をSRGも含めてconsistentに扱う相互作用として、 V. Somà et al., Phys. Rev. C 101, 014318(2020)がある。 下に、\({}^{16}\mathrm{O}\)-\({}^{68}\mathrm{Ni}\)の核子あたりの束縛エネルギーを示した。

NNLOsatとEM1.8/2.0に加えて、上の論文で提案された相互作用NN+3NF(lnl)の結果が示されている。 なお、EM1.8/2.0はIMSRG法による結果で、ほかはADC(3)という、self-consistent Green’s function法の一種による結果である。 A=2,3,4の系から決定したLECsを用いて、非常に精度良く中重核までを記述していることがわかる。
