目次

Emulator/Surrogate model

4. Emulator/Surrogate model

代理モデルの構築は、(他の分野と同様)原子核物理における喫緊の課題である。

原子核物理(とくに理論計算)においては、2010年代になりようやく不定性評価の重要性が認識されるようになり、ベイズ推定などを用いた不定性評価が行われるようになった。 当然ながら、不定性評価を行うためには、計算コストが高い計算を何度も行う(サンプリングする)必要があり、 Full-CI法やPost-HF法などのhigh-fidelityな計算を繰り返し行うことは殆どの場合、現実的ではない。

そこで重要なのが、代理モデルの構築である。 代理モデルは分野によって呼び方は様々だが、emulatorやsurrogate modelなどと呼ばれるのが一般的で、 もう少しクラスを限定して、Reduced order modelやReduced basis modelなどとも呼ばれたりする。

この資料では、核子多体系の構造・反応計算に対して、計算コストを抑えつつ同等の(あるいは数%未満の誤差を許容した)結果を得る方法を ざっくばらんに代理モデルと呼ぶことにする。

4.1. 核子系多体問題の代理モデルを取り巻く動向

原子核物理学において代理モデルが大きく注目をあびるようになったのは、やはり下記の論文が契機と思われる: Eigenvector Continuation with Subspace Learning: D. Frame et al., Phys. Rev. Lett. 121, 032501 (2018)

この論文では、3次元のBose-Hubbard模型及びneutron matterの量子モンテカルロ計算についてEigenvector Continuation(EC)法と呼ばれる方法を用いて、パラメータを幾つか変更して実施した数点の計算結果から、所与のパラメータ点における波動関数やエネルギーを予測する方法を提案したものである。

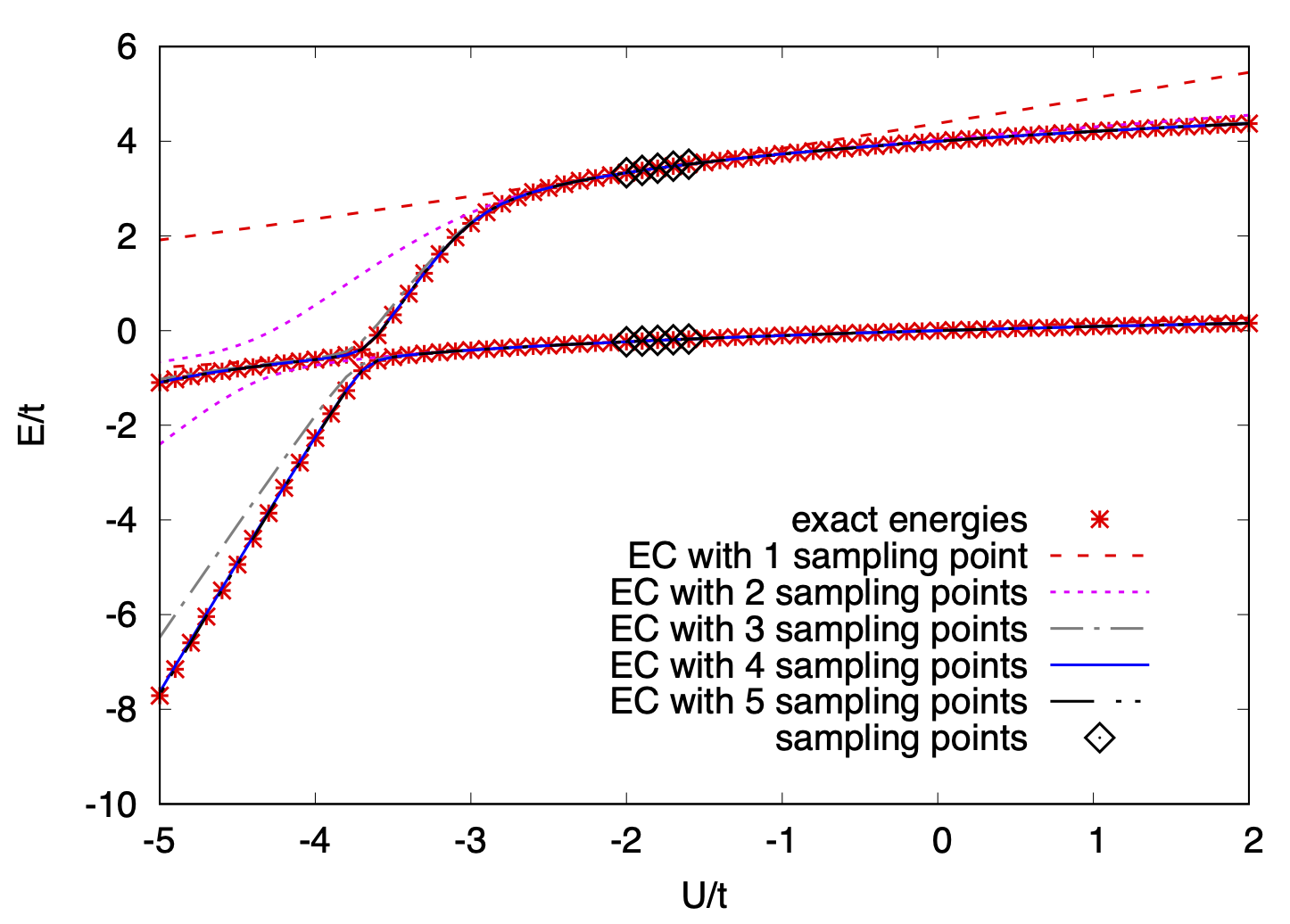
上に示したのは、上記の論文で示された、３次元Bose-Hubbard模型における基底状態と励起状態のエネルギーを、ポテンシャル項\(U\)とホッピング項\(t\)の比に対してプロットした図である。 図中の米?印は厳密解を示し、各線はEC法による予測値を示している。 線の違いは、ひし形で示されているサンプル点の数を示していて、 例えば異なる(最大たったの５点)パラメータ点で得られた２状態の波動関数の情報から、 他の任意のパラメータ点における波動関数を非常に精度良く予測(しかも外挿)できることが示されている。

上記の論文はその後、爆発的に引用され、とくに原子核物理の理論計算コミュニティで、 筆者を含めて構造計算、反応計算の両方において代理モデルの構築が一挙に進む契機となった。

その実、背景にある数学としては特段新しいものではなく、計算物理や応用数学の本に載っている(こともある)Rayleigh-Ritz法や、 Reduced basis methodとして他分野で理解されてきた手法の一種、あるいは再発明とみなすことができる。 とはいえ、流体力学の文脈で提唱された動的モード分解(後述)についても、内部で行う数学的な操作は特異値分解など既知の手法であるが、その提案は2008年であり、歴史は浅い。ある分野で既知とされるような概念でも、他分野で革新的になりえる好例とも言える。

筆者も、CEA-Saclayで2023年6月に行われた国際会議Eigenvector continuation method in nuclear structure and reaction theoryにて招待講演を行うなど、日本国内では少しはこのあたりの動向について理解をしているつもりである。

その後、EC法は原子核物理コミュニティにおいても、Reduced basis methodsというより広い文脈から理解されるようになり、関連する研究が進められている。最近の動向としては、 Rev. Mod. Phys.に投稿中とみられるレビュー論文T.Duguet et al., arXiv:2310.19419などが詳しい。

4.2. Eigenvector Continuation (EC)

ここでは、具体的な問題を挙げることなく、EC法の概要を説明する。 興味のある系のHamiltonianを\(H(c)\)とすると、当然そのSchrödinger方程式は以下のようになる:

\[ H(c) | \psi(c) \rangle = E(c) | \psi(c) \rangle \]

ここで、\(c\)はパラメータである。例えば、\(c\)は上のホッピング項vsポテンシャル項の係数比であるとか、カイラル核力のLow-Energy Constantであるとかをイメージするとよい。

EC法では、この元々の問題をすでに数点解いた結果を用いて、所与のパラメータ点\(c_\odot\)での固有値・固有ベクトルを予測することを考える。 サンプル(ないしsnapshot)の数を\(N_s\)とすると、

\[\begin{split} \begin{align} H(c_1) | \psi(c_1) \rangle & = E(c_1) | \psi(c_1) \rangle \nonumber \\ & \vdots \nonumber \\ H(c_{N_s}) | \psi(c_{N_s}) \rangle & = E(c_{N_s}) | \psi(c_{N_s}) \rangle \nonumber \end{align} \end{split}\]

のそれぞれの波動関数により、\(N_s\)次元の空間を張るベクトルを作ることができる。 この\(N_s\)点のサンプル固有ベクトルを用いて、所与のパラメータの値における固有値問題を近似的に解くには、 以下の一般化固有値問題を考えることになる:

\[ \tilde{H}(c_\odot) \vec{v} = \lambda N \vec{v} \]

ここで、\(\vec{v}\)は\(N_s\)次元のベクトルであり、\(\tilde{H},N\)は\(N_s\)次元の行列で、それぞれ射影空間での\(H(c_\odot)\)の期待値と、サンプル波動関数同士の内積を要素とする行列である。

\[\begin{split} \begin{align} \tilde{H}_{ij} & = \langle \psi(c_i) | H(c_\odot) | \psi(c_j) \rangle \nonumber \\ N_{ij} & = \langle \psi(c_i) | \psi(c_j) \rangle \nonumber \end{align} \end{split}\]

このとき、\(\lambda\)は\(\tilde{H}(c_\odot)\)の固有値の近似値を与え、近似固有ベクトルは

\[ | \psi(c_\odot) \rangle \approx \sum_{i=1}^{N_s} v_i | \psi(c_i) \rangle \]

として与えられる。

このことから、一度サンプル波動関数を得てしまえば、別のパラメータ点で解くべき問題が、元の問題の次元ではなくサンプル数の次元にサイズダウンすることがわかる。 肝心なのは、そうして得られた波動関数がどれほどの精度で元の問題の波動関数を再現できるか、ということであるが、 (問題にもよるが)十程度のサンプル点をえることで、数%以下の誤差で波動関数を再現できることがFull-CI/valence-CI法やCoupled-Cluster法などの計算で報告されている。

なぜこのようなことができるのか、単純化して説明すると、いま考えているHamiltonianのもとで固有値ベクトルは、 naiiveには、サンプル点で得た固有ベクトルが張る低次元空間に十分近いことが予想されるためである。 なぜなら、Hamiltonianにはある程度の対称性や連続性があるため、現実的なパラメータ領域においては、 既に得たサンプルが貼る低次元空間における(一般化)固有ベクトルは、元の問題の波動関数と近いものであると期待される。

実際、EC法は相転移のような特異な領域では、相を跨ぐようなサンプル点を予め用意する必要がある。 順位交差のように、パラメータ領域によって基底状態と励起状態がクロスするような場合にも、 サンプル波動関数のなかに、基底状態と励起状態の両方が含まれるようにすることで、精度良く計算できる。

4.2.1. Eigenvector continuation法を用いた近似殻模型波動関数の構築

配置間相互作用法においてEC法の有用性をいち早く検証したのは、S.König et al., Phys. Lett. B 810, 10, 135814 (2020)で、Full CI法を用いて得られた\({}^4\mathrm{He}\)の基底状態波動関数について、カイラル核力のlow-energy constants (LECs)に対する不定性評価(感度分析)をやってのけた。 これは、EC法なしではとても実現できない計算である。 上記の仕事では、NNLOまでの16個のLECのうち3個のLECに対する不定性の評価を行っている。

その後、筆者らは、より多くのパラメータを含む系(現象論的な相互作用を用いた殻模型計算)でEC法の有用性を検証した→S. Yoshida and Noritaka Shimizu, PTEP 2022 053D02

現象論的な相互作用は、アイソスピン対称性を陽に仮定しても\(sd\)殻で66個、\(pf\)殻で199の1体・2体の行列要素を持つ。 このような多次元のパラメータ空間においても、25-50点程度のサンプル点で、数%以下の誤差で波動関数を再現できることを示した。 また、近似波動関数を構成できれば、それをLanczos法の初期ベクトルとして使うことで、収束性を向上させる前処理的な用途にも使えることを示している。

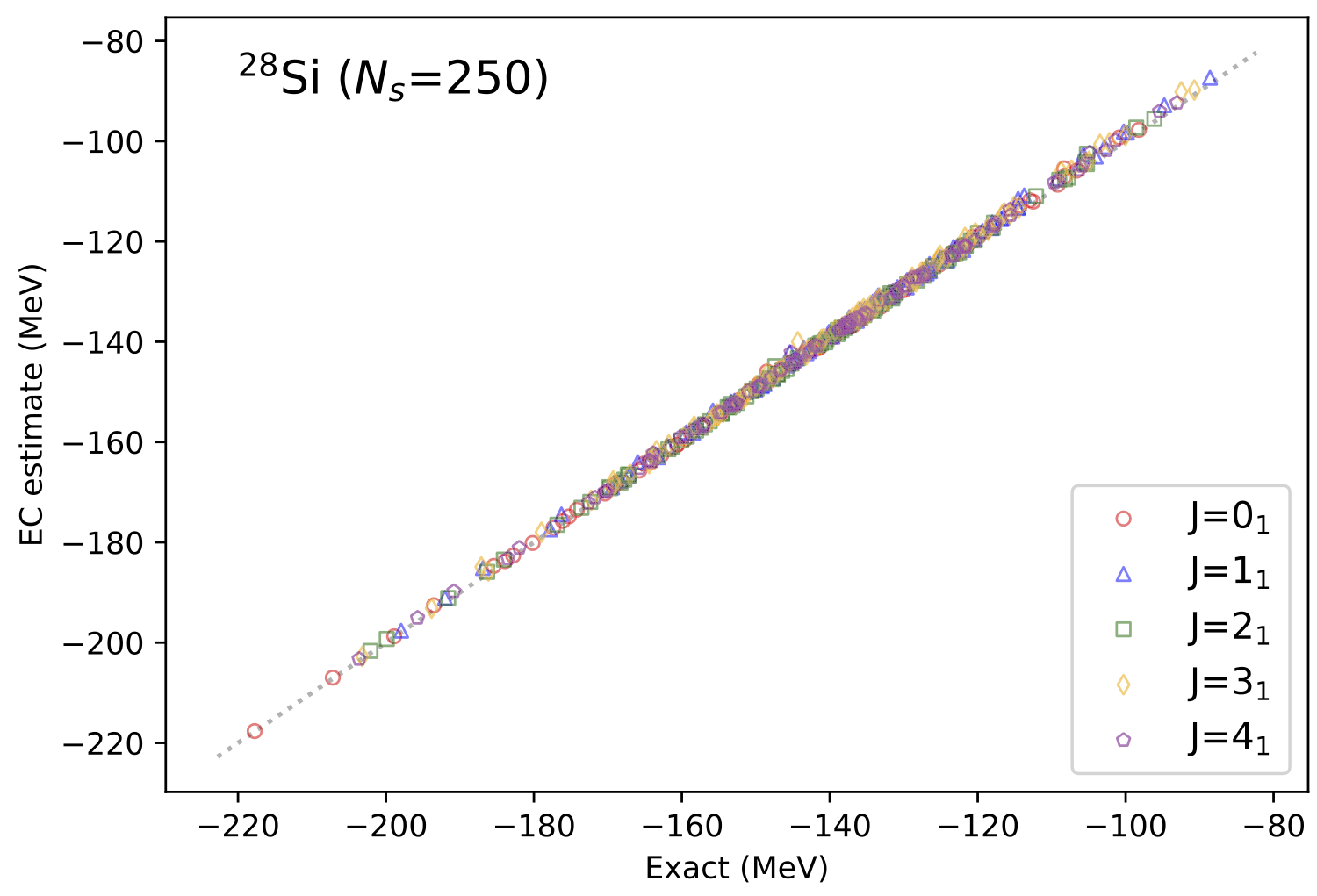
上に、sd殻の殻模型におけるEC法による予測結果を示した。横軸が厳密解、縦軸がEC法による予測値で、ほとんど対角線上に乗っていることがわかる。 ここで対象としている核は\({}^{28}\mathrm{Si}\)で、この核はsd殻において最も大次元\(\approx 90,000\)次元の行列の対角化に対応する。 角運動量の異なる\(J=0,1,2,3,4\)の5つの状態について、50点ほどで波動関数をサンプルしてやれば、 図のように(正規分布やラテン超方格で生成した)ランダムパラメータ(100)点における波動関数を、励起状態も含めて、平均して1%以下の誤差で予測できることが示された。

CI計算は、解くべき問題は一般に大変なものの、Lanczos法の性質上、基底状態とともに励起状態の波動関数も特段の違いなく得ることができるため、 一度サンプル波動関数を構築してしまえば、様々な状態・物理量(電磁遷移行列要素など)を系統的に調べることができる。

有名な殻模型相互作用の波動関数のデータベースを用意しておいて、そこからユーザーは必要な波動関数を取り出して近似波動関数を用いる、 といった方法も将来的にありえるかもしれない。

4.3. データ駆動型アプローチ (機械学習・DMD)

4.3.1. IMSRG-Net: PINNsを用いたIM-SRG法の代理モデル

IM-SRG法は、前章でも説明したように、核子多体系の構造計算において、近年最も注目されている手法の一つである。 (sub-)closed-shell系における基底状態の第一原理的な計算として、Coupled-Clusterとならび非常によく用いられるだけでなく、 Magnus展開を用いた定式化の特性から、模型空間の殻模型相互作用を含む任意の有効演算子を系統的に導出できるという利点を有している。

当然このIM-SRG法についても、パラメータを変えたときの計算結果を得るためには、 何度も大変な計算を繰り返す必要があるため、代理モデルの構築が喫緊の課題となっている。

ここでは、筆者が提案した、IMSRG-Netと呼ばれる手法について説明する。 論文は下記の通り:S. Yoshida Phys. Rev. C 108, 044303 (2023)

IMSRG-Netは、PINNs(Physics Informed Neural Networks)と呼ばれる機械学習の手法を用いて、IM-SRG法の代理モデルを構築するものである。 PINNsとは、物理法則を満たすようにニューラルネットワークのパラメータを学習する手法であり、 一言で簡単に言えば「誤差関数に系を支配する微分方程式(ODE/PDE)を入れてしまえば物理法則を満たすように学習してくれるのでは？」というアイデアである。 「物理法則を満たすように」というのはやや言い過ぎで、実際に誤差関数として入れるのは、 データ点で対象とする値が、微分方程式の解であることを要求するようなソフトなconstraintである。

幸い、IM-SRG法はflow方程式という形の常微分方程式(ODE)であるため、PINNsを適用して遊んでみるのは、わりと自明である。 下に模式図を示した。

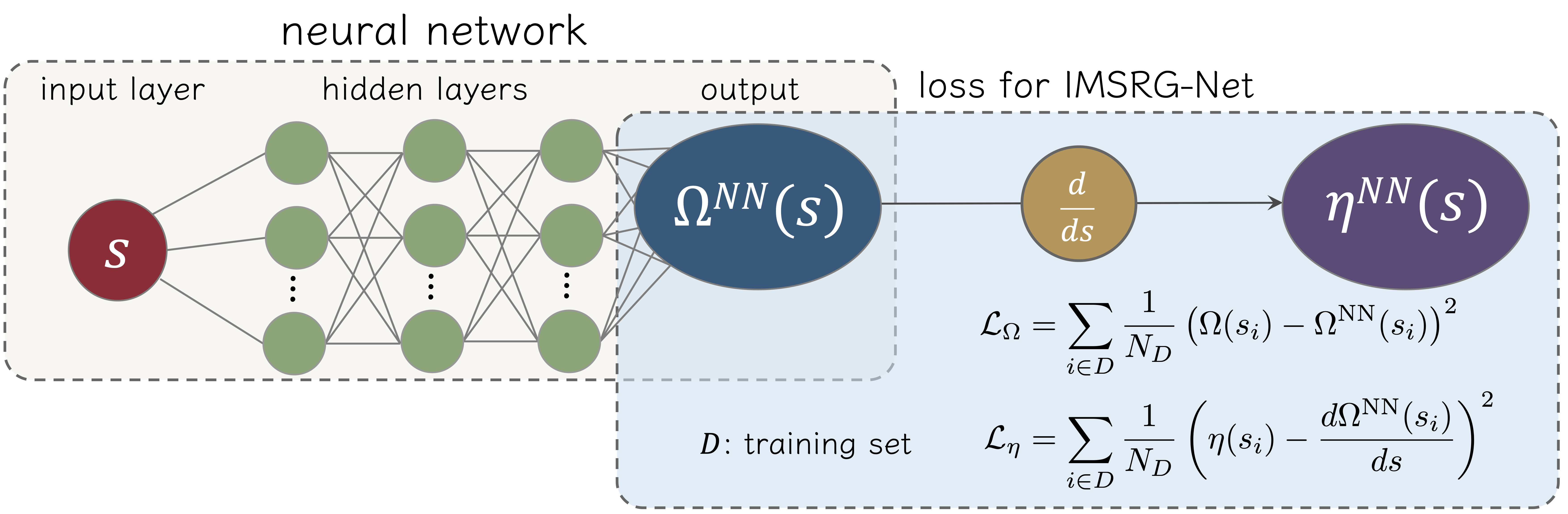
まずニューラルネットワークの構造は、最も基本的な全結合のニューラルネットワークを用いる(もちろんもっと複雑な構造を用いてもよいはずだが)。 入力は、IM-SRG法のflow parameterである\(s\)で、出力は、IM-SRG法(そのとくにMagnus展開を用いるformulation)のユニタリ変換を与えるMagnus operator \(\Omega(s)\)である。

ニューラルネットワークが計算の各ステップ\(s\)で得られるデータ\(\Omega(s)\)を幾つか与えるだけで、\(s\to\infty\)での\(\Omega(s)\)を予測するように学習できればそんなに嬉しいことはないが、もちろんそう上手くは行かない。 そこで、IM-SRG法のflow方程式を、ニューラルネットワークの誤差関数に入れて、 \(\Omega(s)\)の\(s\)に関する微分方程式(の第１近似)を誤差関数に入れることで、 ニューラルネットワークがflow方程式を近似的に満たすように学習するようにする。

\(d\Omega(s)/ds\)は、ネットワークの出力に対する入力の微分であるため、 自動微分や数値微分を用いて効率的に計算することができる。 IMSRG法では、出力が大次元のため、自動微分の計算が大変なため、数値微分を用いている。

こうした物理のドメイン知識を機械学習モデルに入れる際、よくあるのが、アーキテクチャ側を工夫する方法で、 例えば画像認識の基本的なアルゴリズムとしてよく用いられるCNN(Convolutional Neural Network)は、 画像の回転や並進に対して不変な特徴量を抽出するように設計されている。 一方で、PINNsは誤差関数に物理のドメイン知識を入れることで、探索すべきパラメータ空間を制限している方法と言える。

\(s\)が比較的小さい領域では、flow方程式はかなり非線形性が強いため、\(s \to \infty \)での値を予測する外挿の精度は、 当然悪くなってしまうが、ある一定の\(s\)までをデータ(snapshot)として与えることで、その後の計算をPINNsで省略できることがわかった。

高速化としては、たかだか数10%程度であるが、それでも、PINNsを用いてIM-SRG法の計算コストを削減できることがわかった。 また、\(\eta(s=\infty) \to 0\)という、IMSRG flow方程式の漸近的な振る舞いが学習の過程で自然に満たされるため、 外挿の安定性が高いのもこの提案手法の特徴である。

4.3.2. 動的モード分解

動的モード分解は、2008年にP.J. Schmidらによって提唱された手法であり、 時空間に依存するデータを用いて、そのデータを生成する力学系の特徴を抽出する手法である。 Journal of Fluid Mechanicsに出版されたDynamic mode decomposition of numerical and experimental dataは3000の引用を超える。

動的モード分解(DMD)の基本

元々がメッシュ点で与えられた行列やテンソルなど多次元配列だとしても、一定の規則に基づいてベクトル化していると考えてほしい。

時間方向に対する\(N+1\)点のスナップショットが与えられたとする:\(\{ \mathbf{x}_1, \ldots, \mathbf{x}_{N+1} \}\) ここで、\(\mathbf{x}_i\in\mathbb{R}^d\)は、\(d\)次元のベクトルである。 次に、それらスナップショットから構成される以下の\(d\times N\)行列を考える

\[\begin{split} \mathbf{X} := \begin{pmatrix} | & & | \\ \mathbf{x}_1 & \cdots &\mathbf{x}_N \\ | & & | \end{pmatrix} , \hspace{0.5cm} \mathbf{Y} := \begin{pmatrix} | & & | \\ \mathbf{x}_2 & \cdots &\mathbf{x}_{N+1} \\ | & & | \end{pmatrix} \end{split}\]

一般に、\(\mathbf{X}\)と\(\mathbf{Y}\)は、以下のような関係にある:

\[ \mathbf{Y}=\mathbf{F}(\mathbf{X}) \]

ここで、\(\mathbf{F}\)は、\(\mathbb{R}^d\)から\(\mathbb{R}^d\)への写像(時間発展１ステップの操作とみなせる)で、非線形な関数の場合が多い。 最もよくある場合としては、偏微分方程式に従う系だろうか。

一般に大次元の系では、偏微分方程式を数値的に解くのがかなり大変で、何らかの方法で、系の時間発展を近似することも必要になる。

DMDでは、この1ステップの時間発展を、線形写像\(\mathbf{A}\)を用いて近似する事を考える:

\[ \mathbf{Y}\approx\mathbf{A}\mathbf{X} \]

もし上式の近似が良い近似であれば、系の時間発展を線形演算\(\mathbf{A}\)で効率よく近似出来ると期待される。 以降で見るように、DMDでは、データ(スナップショット)から\(\mathbf{A}\)を求めるので、equation freeな手法である。

"良い近似"では、曖昧なので、\(A\)の推定問題をFrobeniusノルムを用いて、以下の最小化問題と定義する:

\[ \mathrm{min}_{\mathbf{A}}\|\mathbf{Y}-\mathbf{A}\mathbf{X}\|_F^2 \]

もちろん、Moore-Penroseの擬似逆行列\(X^+=V\Sigma^{-1}U^t\)を用いて、\(A=YX^+\)として理論上は求めることができるが、 注目するダイナミクスが大次元である場合、計算コストが高くなると予想される。

DMDでは、データの次元\(d\)に比べて小さい\(r\)次元に射影したダイナミクスを考えることで、 \(A\)の推定問題を少ない計算量で置き換え、系のダイナミクスを詳細に解析しやすくする、というのが基本的な発想となる。

DMDのアルゴリズム

データが実数であることを仮定して転置で書いてあるが、複素行列の場合は随伴に置き換えれば良い。

DMDの基本的なアルゴリズムは以下の通りである:

  1. データ行列\(\mathbf{X}\)を特異値分解する:

    \[ X = U\Sigma V^t \]

    ここで、\(U\in\mathbb{R}^{d\times k}\), \(\Sigma\in\mathbb{R}^{k\times k}\), \(V^t \in\mathbb{R}^{k \times N}\)で、 \(k \leq \mathrm{rank}(X) \leq \mathrm{min}(d,N)\)である。

  2. \(U,\Sigma,V\)の低ランク近似 \(r \ll \mathrm{min}(d,N) \)を考える:

    \[ U_r \equiv U(:,1:r), \Sigma_r \equiv \Sigma(1:r,1:r), V_r \equiv V(:,1:r) \]

  3. 以下の\(r \times r\)行列を考える:

    \[ \tilde{A} = U^t_r A' U_r \]

    ただし、

    \[ A' = Y V_r \Sigma^{-1}_r U^t \]

    で、この\(A'\)が意味するところは、\(YX^+(=YV\Sigma^{-1}U^t)\)の低ランク近似である。

  4. \(\tilde{A}\)の固有値\(\lambda_i\in \mathbb{C}\)と固有ベクトル\(\mathbf{w}_i \in \mathbb{C}^r\)を求める。

    \[ \tilde{A} w_j = \lambda_j w_j \]

  5. それぞれの固有値に対して、以下の\(d\)次元ベクトルを計算する:

    \[ \phi_j = \lambda_j^{-1} Y V_r \Sigma_r^{-1} w_j \]

    これらをexact DMD modesと呼ぶ。あるいは、このexact DMD modesのかわりに\(d\)次元ベクトル

    \[ \xi_j = U_r w_j \]

    を計算することもある。これは、exact DMD mode \(\phi_j\)の近似に相当し、\(\xi_i\)の集合をprojected DMD modesと呼ぶ。

まず1.で元のダイナミクスの低次元表現を得た後、 3.では、その射影空間における時間発展(ユニタリ変換)の形となっている。 4.の固有値解析においては、元の\(A \in \mathbb{R}^{d\times d}\)に対する近似として、 \(\tilde{A}\in \mathbb{R}^{r\times r}\)の固有値解析を行っており、\(r \ll d\)の場合に大幅な計算コストの削減が見込める。

このとき、重要な性質として、以下のようなものがある:

  • \(\tilde{A}\)の非ゼロ固有値は、\(A'\)の固有値に一致する

  • exact DMD modes\(\{ \phi_j \}\)が\(A'\)の固有ベクトルとなる

1.において、データ行列\(\mathbf{X}\)の特異値分解を行うが、full rank SVDが大変な場合は、 truncated SVDと呼ばれるような、主要な特異値を取り出す方法を考えると良い。

full rank SVDについては、LinearAlgebra.jlのsvd関数を用いればよいが、 truncated SVDについては、Arpack.jlないしKrylovKit.jlなど、Krylov部分空間法を用いたパッケージを用いれば良い。

#使用するパッケージをインストールしておこう (1回実行すればよいため、コメントアウトしておいた)
# using Pkg 
# Pkg.add("Arpack")
# Pkg.add("KrylovKit")

using LinearAlgebra 
using Arpack
using KrylovKit

n = 500
A = randn(n,n)

# LinearAlgebra.svd(A)
U, S, V = svd(A)

# Arpack.svds(A; nsv=10)
Z = svds(A; nsv=5)

# KrylovKit.svds(A, nsv)
vals, lvecs, rvecs = svdsolve(A, 5)

println("LinearAlgebra: ", map(x->round(x, digits=8), S[1:5]))
println("Arpack:        ", map(x->round(x, digits=8),Z[1].S[1:5]))
println("KrylovKit:     ", map(x->round(x, digits=8),vals[1:5]))

時系列データの再構成

上で記載したDMDモードと初期値\(x_1\)を用いて、時刻\(k\)におけるデータを再構成する方法を考えよう。

まず、時刻\(k\)における推定値\(\mathbf{x}_k\)は、以下のように計算される:

\[ \mathbf{x}_k = A \mathbf{x}_{k-1} = \mathbf{A}^{k-1} \mathbf{x}_1 \]

これを、元の\(d\)次元の問題から、\(r << d\)次元の問題に変換するために、

\[ \mathbf{z}_k \equiv U^t \mathbf{x}_k \]

を導入すると、\(\mathbf{x}\)の時間発展は、潜在空間での表現\(\mathbf{z}\)の時間発展に書き直すことができる。

\[\begin{split} \begin{align} U_r \mathbf{z}_{k+1} &= A U_r \mathbf{z}_k = (U_r \tilde{A} U^t_r)^k U^t_r \mathbf{z}_k = U_r \tilde{\Lambda}^k \mathbf{z}_k \nonumber \\ \mathbf{z}_{k+1} &= \tilde{A}^k \mathbf{z}_1 \nonumber \end{align} \end{split}\]

2024年6月にFRIBでセミナーをする機会を頂いたので、現地で議論しながら関連する仕事を進めたい。乞うご期待。

DMDをIMSRG法に応用するアイデアは、ミシガン州立大&FRIB(Facility for Rare Isotope Beams)グループで提案された。 NuclearToolkit.jlには、DMDを用いて、IM-SRG法の代理モデルを構築するための関数が用意されている。

DMDの有名な教科書(Kutzら)にある、流体力学(Kármán渦)の例を扱うサンプルJuliaコードを用意しておいた。 気になる方はこちらからどうぞ。

4.4. 核子系の量子計算

量子計算を代理モデルと呼ぶのは不適当とも思うが、関連の話題として言及しておくことにする。

先の、殻模型/配置間相互作用法の章でも述べたように、微視的な核構造計算として強力なツールであるCI法だが、 その計算コストは考えるべき自由度に対して指数関数的に増大する、という困難を抱えている。 これは、核子系に限らず、電子系などにおいても同様である。

当然、物性物理や量子化学分野と同様、原子核物理においても、量子計算の応用が期待されており、 必要なリソースの見積もりや簡単な系のシミュレータ・実機における計算なども多数報告されている。

筆者も現在、核子系の量子計算の研究を東大・理研グループと共同で進めており、数日後の日本物理学会においても発表を行う →18pU2-11。 是非お越しください!(宣伝)

前へ

3. 殻模型(配置間相互作用法)