目次

殻模型(配置間相互作用法)

3. 殻模型(配置間相互作用法)

この章では、核構造計算の最も基礎となる殻模型について説明する。

3.1. 用語の説明

殻模型(shell model)は"かくもけい"と呼ぶ人もいるが、専門家は"からもけい"と呼ぶ事が多い。 "核模型"と区別するためなのか、歴史的な経緯があるのか筆者は知らない。

殻模型(shell model)というと、分野外の人は、Mayer-Jensenの殻模型(1963年 ノーベル物理学賞)を思い浮かべると思われる。 例えば、猪木・川合 量子力学Ⅱなどの教科書にも載っている、魔法数(閉殻構造を与える核子数)の説明を与えたものである。

一方で、現代の原子核分野では、殻模型というと、閉殻芯を仮定し、限られたバレンス(valence)軌道を activateした空間内での(厳密ないし漸近的に厳密な)対角化計算を指すのが一般的である。 量子化学分野などでいうところの、配置間相互作用法・configuration interaction (CI)計算に相当する。 この章でも、殻模型という言葉はこの意味で用いることにする。

関連する用語として、閉殻芯の存在を仮定せず、全ての核子の自由度を陽に扱うFull-CI計算のことを、 原子核分野ではno-core shell model (NCSM)と呼ぶ。

また、模型空間やmodel spaceという語句も良く用いられるが、これは上述のようなactivateされた軌道を指す。あるいは、「\(0f7/2\)の占有数を最小4,最大8の配位に限定して考える」といったような、模型空間を限定することもあり、こうしたtruncationも含めて、模型空間と呼ぶこともある。

3.2. jj-coupling軌道と魔法数

前述の魔法数を説明する上で重要なのが、軌道角運動量\(\ell\)と合成角運動量\(j\)である。

核子が、平均的なポテンシャルの中で一粒子運動をしているという描像から、 Mayer-Jensenは、スピン・軌道力(LS力)を導入することによって、 安定な構造を示す核子の数、魔法数(2, 8, 20, 28, 50, 82, 126)を説明した。

下に、魔法数の模式図を示す。

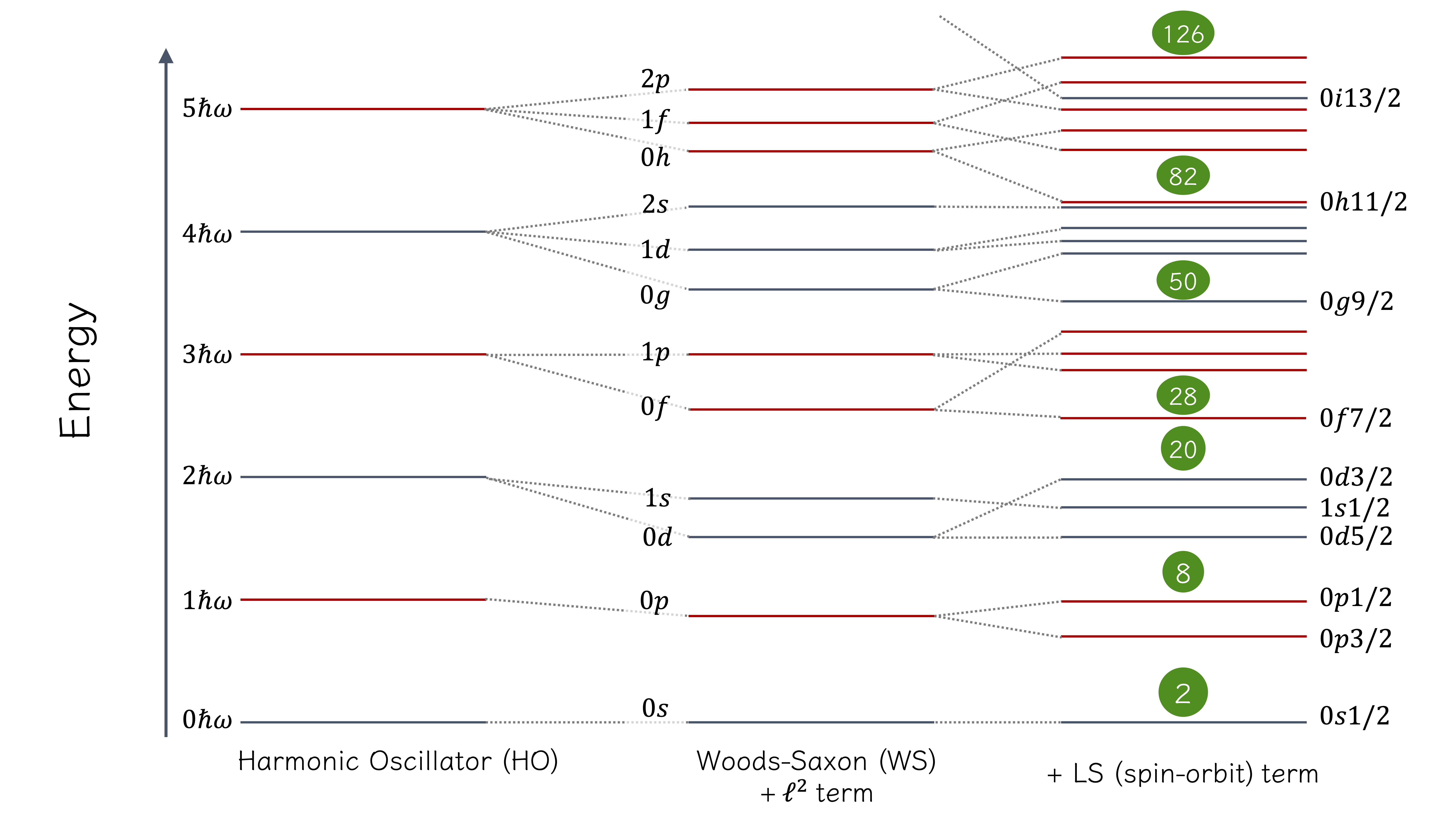
この図における、各一粒子軌道の並び順には、特に意味はない。 実際の原子核では、変形の効果や、核力の機微によって、軌道の順位が変わることで、 魔法数が消失したり、新たな魔法数が発現することがある。 核力におけるペアリング相関の強さから、\(j\)の値が大きい軌道が、魔法数の形成に寄与することが多い。

例えば(図左側)3次元の等方調和振動子ポテンシャルで運動する粒子の場合、エネルギー準位は、 主量子数\(n\)に対して、\(E_n=(n+3/2)\hbar\omega\)となる。 零点振動エネルギーのことを一旦忘れて、\(n=0,1,2,3,\cdots\)となるエネルギー準位が、 それぞれ\(0\hbar\omega, 1\hbar\omega, 2\hbar\omega, 3\hbar\omega,\cdots\)となる。 このポテンシャルに、軌道角運動量\(\ell\)に依存する項\(C \ell^2\)を加えると、 それぞれのエネルギー準位は\(\ell\)の値に応じて、分離する。 また、\(\ell\)とスピン角運動量\(s\)の合成角運動量\(j\)に依存する項\(C' \ell \cdot s\)を加えると、 合成の角運動量\(j\)に依存して、さらに縮退が解ける(順位が分離する)。 この効果が、魔法数を与える上で重要になる。

また、近年の理論・実験研究によって、中性子過剰(あるいは陽子過剰)な不安定原子核領域においては、 従来の魔法数が消失したり、新たな魔法数が発現することが明らかになってきている。 このことは、Nilsonダイアグラムからは、変形の効果として理解することもできるし、 現代的な大規模殻模型計算によって、実際に微視的な機構(テンソル力や有効核力の各成分の機微)からの理解も進んでいる。 例えば、筆者も(文字通り末席に)参画している研究で言うと、下記のものなどがある。

"調和振動子"というと、上図の左のように、3次元の等方調和振動子ポテンシャルを指すことが多いように思うが、 第一原理計算やCI計算を専門とする人の多くにとっては、調和振動子(基底)というと、 既に軌道角運動量\(\ell\)や合成角運動量\(j\)が与えられ、軌道が分離している状況を想像する人が多い(と思う)。 筆者は、このことが原因で、平均場理論やDFTが得意な研究者に誤解を与えてすれ違いコントになってしまった経験がある。

殻模型(に限らないが)では、核子の状態を表す表示として、通常、調和振動子(harmonic oscillator; HO)基底を用いる。 \(n,l,j\)をそれぞれ、主量子数、軌道角運動量、全角運動量として、\(n,l,j\)、そしてprotonとneutronの区別を明示するために、 \(t_z\)を用いて、\(n,l,j,t_z\)で軌道をラベル付けする。

主殻(major-shell)は\(e=2n+l\)によって決まる。 例えば、\(n=e=0\)の場合、\(l=0\)のみが許され、\(j=1/2\)となるため、\(0s\)軌道と呼ばれる。 \(e=1\)の場合も、\(n\)は0のみが許され、\(l=1\)のみが許されるため、\(0p\)軌道(\(0p_{1/2}\)と\(0p_{3/2}\))と呼ばれる。 \(e=2\)の場合は、\(n=0,1\)が許され、それぞれ\(l=2,0\)が許されるため、\(1s0d\)軌道(\(1s_{1/2}, 0d_{3/2}, 0d_{5/2}\))と呼ばれ、 分野においては、単に\(sd\)軌道と呼ばれるのがほとんどである。以後同様。

3.3. 殻模型の概要

殻模型の基本的な考え方は、対象とする原子核が、閉殻芯と少数のバレンス核子からなる系であると仮定し、それらの自由度のみからその構造を記述することを目的とするものである。

もちろん、全ての原子核でこのような仮定が成り立つ訳では無いが、70年代来から今日に至るまで、原子核の構造を記述するための基本的な手法として、殻模型が用いられてきたという背景がある。なかでも特に顕著な成功事例が安定核近傍の原子核である。

例えば、\(sd\) shellと呼ばれる\(1s_{1/2},0d_{3/2},0d_{5/2}\)の3つの軌道をバレンス空間として用いた計算は、 \(^{16}\mathrm{O}\) を閉殻芯として、Z=8-20, N=8-20の \({}^{40}\mathrm{Ca}\) までの原子核を表現することができる。

例として、\({}^{24}\mathrm{Mg}\) という、陽子・中性子ともに12個の原子核を考える。 マグネシウム同位体のうち自然界の約8割近くが、この\({}^{24}\mathrm{Mg}\) (N=12)である。 この\({}^{24}\mathrm{Mg}\) を、24体系として解こうとするのは無理筋である。 だが、この核を安定核である\({}^{16}\mathrm{O}\)を閉殻芯として、 バレンス核子を4個の陽子と4個の中性子の"バレンス"核子を有効な自由度として扱うことで、 いささか扱いやすくする、というのが殻模型の基本的な考え方である。

細かいことを言えば、Full-CIなど2を超える複数主殻を扱う場合には、one-bodyの項で、 非対角成分\(h_{ab}\)を陽に考える必要がある。 2体力部分は、「平均場に取り込めない相互作用」という意味で、残留相互作用という言葉もよく用いられてきた。

上で導入した調和振動子基底のラベル\(\{n,l,j,tz\}\)を用いて、殻模型のハミルトニアンは、

\[ H = \sum_{i} \langle h_i \rangle a^\dagger_i a_i + \frac{1}{4} \sum_{ijkl} \langle ij | v | kl \rangle a^\dagger_i a^\dagger_j a_l a_k \]

と書くことができる。\(h_i \equiv \langle i | h | i \rangle\)は、一粒子軌道\(i\)のsingle-particle energy (SPE)であり、 \(\langle ij | v | kl \rangle\)は、two-body matrix element (TBME)と呼ばれ、 バレンス核子間に働く2体の相互作用を表す。

理論に含まれるパラメータは、SPEとTBMEのみであるため、あとは後述のように適切な状態ベクトルを作って、対角化すれば良い。 では、これらのSPEとTBMEはどのようにして決められるだろうか？

3.4. 有効相互作用理論

殻模型で用いられるバレンス核子間に働く相互作用は、閉殻芯の存在により、 いわば媒質中の核力とも呼ぶべきものであり、free-spaceの核子間相互作用とは異なる。 このような相互作用を、有効相互作用(effective interaction)や有効核力と呼ぶこともある。

当然、この有効相互作用は、本来free-spaceの核子間相互作用を元にして構成されるべきものと期待されるが、 一方で、これまでの現象論的な研究の成功の歴史もあり、それと同程度の精度を持つ有効相互作用を核力から 構成することが困難であることも知られている。

核力から有効相互作用を導出する方法として代表的なものを幾つか挙げておく:

  • 多体摂動論(Many-body perturbation theory; MBPT)

  • Unitary correlation operator method (UCOM)

  • Coupled-Cluster (CC)

  • In-medium similarity renormalization group (IM-SRG)

こうした第一原理的な方法による有効相互作用(あるいはハミルトニアンに限定せず有効演算子)の導出は、 今なお国際的にもホットな研究トピックの一つであり、筆者もその分野で研究を行っている一人である。

一方で、1960年以降の半世紀近くにわたって、現象論的なアプローチ「基底状態エネルギーや(low-lyingな)励起状態に対して、SPEやTBMEをfitする」 が幅広い原子核(とくに安定核近傍)の性質を非常に精度良く記述することができることが報告されてきた。

このような方法によって構成された有効相互作用を前者と区別する意味で、現象論的やphenomenologicalと呼ぶことがある。 もちろん、実験データが無い領域では現象論的に相互作用を決定することも困難なため、前述の方法とは相補的な関係にある。

現象論的な有効相互作用による計算の成功を示す特徴的な仕事として、前述のsd-shell領域における有効相互作用として、USD(Universal sd shell) interaction及びそれらを拡張したUSDB(USDAもある)相互作用などが知られている。

USDBでは、\({}^{16}\mathrm{O}\)--\({}^{40}\mathrm{Ca}\) 領域の基底状態・励起状態の実験値を用いて有効相互作用をfitすることで、 root-mean-square(rms)値にして200 keV以下の高精度で幅広い原子核を記述することができる事がわかっている。

もちろん、\(^{16}\mathrm{O}\) コアからの励起が重要な原子核・状態について、\(sd\) shellのバレンス空間のみでの記述では不十分な場合も多くある。 そうした状態はfitの場合には除外されたり、有効相互作用の評価の際にも除外されることが多いことには留意が必要であるが、 少なくとも安定核近傍の酸素-カルシウム同位体の基底状態エネルギー・(低エネルギー領域の)励起スペクトル, 電磁遷移, ベータ崩壊などの量を 広範にわたって殻模型以上に高精度で記述する方法は、現在のところ存在しない。その意味でよくUSD(B)を用いた計算は、ゴールドスタンダードと称される。

3.5. 殻模型計算の実際

もう少し計算の具体的な中身をイメージするために、実際のコードの中でどのような計算が行われているのかを説明する。

簡単のため、以下では、\(^{4}\mathrm{He}\)を閉殻芯とした、 proton-neutronのバレンス2体系である\({}^{6}\mathrm{Li}\) (Z=N=3)を考えてみよう。

軌道という際には、\(\{n,\ell,j,t_z\}\)の足なのか、\(\{n,\ell,j,j_z,t_z\}\)の足なのかをきちんと区別する必要があるが、適宜文脈から判断してもらいたい。

この場合、バレンス空間は、\(0p_{1/2}\)と\(0p_{3/2}\)の2つのjj-coupling軌道からなる。 軌道内の\(j_z\)で区別される状態の数は、それぞれ\(2j+1\)であるため、\(p_{1/2}\)なら２つ、\(p_{3/2}\)なら４つの状態が存在する.

さらに、陽子・中性子を明示的に区別する(proton-neutron formalism)で言うなら、軌道の数は合計で6×2の12個ということになる。

さて、\({}^{6}\mathrm{Li}\)という原子核の状態(配位)を表現するためには、

\[ | 000001 \rangle_p \otimes | 000001 \rangle_n \]

のように、陽子・中性子のそれぞれの軌道の数だけビット列を用意し、配位を表す状態ベクトルを用意してやれば良い。 0が非占有, 1が占有されている軌道を表す。

今(弱い相互作用は考えず、陽子・中性子の数は変化しないので)、\({}^6\mathrm{Li}\)の陽子・中性子それぞれの状態を表すビット列は必ず、どれか一つだけがbitが立っていて、それ以外は0であるような状態になる。当然、許される配位の数は全部で、\(6^2=36\)個となる。

この全てを考えてももちろん構わないのだが、実際には(有効)核力の持つ対称性から、 \(j_z\)の和が0(奇数個の核子からなる核の場合は1/2)の状態のみを考えれば、その中に全ての状態の情報が含まれる。

したがって、\({}^6\mathrm{Li}\)の状態を表現するためには、状態の角運動量\(J\)が幾つであろうと、 \(\sum j_z = 0\)を満たすような状態のみを考えれば良く、その数は10個となる。 下に模式図を示した。

\(j_z\)の和を用いて状態を指定する計算方法はいわゆる\(M\)-schemeと呼ばれるもので、 もしも\(J=J'\)のみの状態だけがほしいのであれば、全核子の\(j_z\)の合計が\(J'\)になる配位だけを考えれば良い。 殻模型で、対角化すべき行列の次元、という際には、この\(M\)-schemeの元での配位の数を指すことが多い。

proton, neutronのそれぞれの配位の\(j_z\)の合計が\(M_{p}\), \(M_{n}\)であるとすると、 \(M_p + M_n = 0 \) (奇核の場合は\(1/2\))となる配位を考えれば良いことになる。

この\(M\)-schemeの下で陽に扱うべきproton(neutron)の配位が\(N_p\)(\(N_n\))個あるとすると、興味のある原子核の状態は、 \(N_p \times N_n\)個存在することになる。

\[ | \psi \rangle = C_{ij} | i \rangle_p \otimes | j \rangle_n \]

\(i,j\)はそれぞれ、proton, neutronの配位を表すビット列(ないしそれに対応する整数)である。

このとき、殻模型のハミルトニアンの2体力部分は、proton-proton, neutron-neutron, proton-neutronの3つの項に分かれる。 (\({}^{6}\mathrm{Li}\)の場合は当然、proton-neutron力のみが効く)。 pp, nnの項は、それぞれneutron側の状態, proton側の状態を区別しないので、別々に考えられる。 proton-neutronの項の場合は、proton側の状態とneutron側の状態の組み合わせを考える必要があるため、一般に考慮すべき項の数が多くなる。

扱うバレンス核子の数が少なければ、\(M_d = N_p \times N_n\)の行列を明示的に作成してそれを対角化しても良いのだが、 多くの興味のある問題の場合、行列要素を明示的に保持して対角化することは非現実的となる。

一般に、殻模型におけるハミルトニアン行列\(\langle \psi| \hat{H} | \psi \rangle \)の非零要素の数は、\(M_d\)よりもぐっと小さくなる(スパースである)。 そこで、行列要素を陽に保持するのではなく、必要なときに行列要素を計算 or 参照する方法を用いる。

また、実際の計算では、行列を対角化するのではなく、比較的少数のlow-lyingな(＝エネルギーが低い)固有値・固有ベクトルを求めることが殆どである。その際にはLanczos法をはじめ、Krylov部分空間を用いた反復対角化法による計算が主流となる。

Lanczos法は、「20世紀のトップ10アルゴリズム」の一つ、Krylov部分空間法に属するアルゴリズムであり、 実対称行列の最大(最小)固有値・固有ベクトルを求めるためのアルゴリズムである。 Lanczos法では、試行関数\(|\psi_0\rangle\)に対して、Hamiltonianを順次作用させて得られるベクトルを用いて、

\[ \{ |\psi_0\rangle, H|\psi_0\rangle, H^2|\psi_0\rangle, \cdots \} \]

というKrylov部分空間を作り、その中での固有値・固有ベクトルを求める。 \(H\)を繰り返し作用させることで、Krylov部分空間は次第に \(H\)の絶対値最大の固有値に対応する固有ベクトルの成分が増幅されるようになり、 比較的少数の反復で、固有値・固有ベクトルを得ることができる。 また、励起状態の計算についても、直交化のコストや収束判定に必要な反復回数の増加はあるものの、 基底状態の計算と特段変わらない手順で自然に計算することができる。

3.5.1. 行列要素の詳細

殻模型コードのインプットファイルには、SPEとTBMEの情報が含まれているが、ここでのTBMEは、

\[ \langle a b | v | c d \rangle_J \]

のように、4つの一粒子軌道に対応したラベル\(a,b,c,d\)と、合成角運動量\(J\)、対応する行列要素の値を含んでいる。 この行列要素と、一般的な2体相互作用を持つHamitonianの表式との対応関係を示しておこう。 適当な量子数を持つ2粒子の状態を

\[ | \alpha \beta \rangle = a^\dagger_\alpha a^\dagger_\beta | 0 \rangle \]

と書いたとすると、ハミルトニアンは前述のように

\[ H = \sum_{\alpha} \langle h_\alpha \rangle a^\dagger_\alpha a_\alpha + \frac{1}{4} \sum_{\alpha\beta\gamma\delta} \langle \alpha \beta | v | \gamma \delta \rangle a^\dagger_\alpha a^\dagger_\beta a_\delta a_\gamma \]

とかける。これらの一粒子軌道が、\(jj\)-couplingの意味での調和振動子に対応するとしよう。つまり\(\{n, \ell, j, t_z\}\)でラベル付けできる。 ２核子対の状態は、合成の角運動量\(J\)とその\(z\)成分\(M\)によって展開することができ、

\[\begin{split} \begin{align} |\alpha \beta \rangle = a^\dagger_\alpha a^\dagger_\beta | 0 \rangle &= \sum_{JM} (j_a m_\alpha j_b m_\beta | J M ) [ a^\dagger_a a^\dagger_b]_{JM} |0 \rangle \nonumber \\ N_{ab}(J) &= \frac{\sqrt{1+\delta_{ab}(-1)^J}}{1+\delta_{ab}} \nonumber \end{align} \end{split}\]

とかける。ただし、デルタ関数は\(\{ n,l,j, t_z\}\)に対して取る。

\[ | ab; JM \rangle \equiv N_{ab}(J) [ a^\dagger_a a^\dagger_b]_{JM} |0 \rangle \]

とすると、

\[\begin{split} \begin{align} |\alpha \beta \rangle = a^\dagger_\alpha a^\dagger_\beta | 0 \rangle &= \sum_{JM} (j_a m_a j_b m_b | J M ) [ a^\dagger_a a^\dagger_b]_{JM} |0 \rangle \nonumber \\ N_{ab}(J) &= \frac{\sqrt{1+\delta_{ab}(-1)^J}}{1+\delta_{ab}} \nonumber \end{align} \end{split}\]
\[ | \alpha \beta \rangle = \sum_{JM} (j_a m_a j_b m_b | J M ) [ a^\dagger_a a^\dagger_b]_{JM} |0 \rangle = \sum_{JM} (j_a m_a j_b m_b | J M ) N^{-1}_{ab}(J) | ab; JM \rangle \]

2体相互作用部分を整理すると

\[ \sum_{\alpha \beta \gamma \delta} \langle \alpha \beta | V | \gamma \delta \rangle = \sum_{abcd} \sum_{JMJ'M'} (j_a m_a j_b m_b | J M ) (j_c m_c j_d m_d | J' M' ) N^{-1}_{ab}(J) N^{-1}_{cd}(J') \langle ab; JM | V | cd; J'M' \rangle \]

さらにいうと、核子間の相互作用は、既約テンソルの言葉でスカラーであるため、

\[ \langle ab; JM | V | cd; J'M' \rangle = \delta_{JJ'} \delta_{MM'} ( ab; JM || V || cd; JM ) \]

となる。殻模型の相互作用ファイルには、右辺の換算行列要素に対応する値が記録されている。 実際には、コード内で、\(H|\psi\rangle\)などの演算を行う際には、\(m_a, m_b\)など\(j_z\)の足を陽に持つ行列要素をあらかじめ保持したり、 on the flyで計算して使ったりと、実装は様々である。殻模型コードの実装のより詳細については例えば下記の文献が詳しい。

3.5.2. \({}^{24}\mathrm{Mg}\)の計算例

NuclearToolkit.jlには、殻模型関数のメインAPIとして、main_sm関数が用意されていて、 相互作用ファイルのパス, 対象とする核(文字列か、[Z,N]の配列)、固有値の数、対象とする\(J\)の値などを指定することで、 殻模型計算を行うことができる。

ここで、幾つかの相互作用を用いて、\({}^{24}\mathrm{Mg}\)の計算を行ってみよう。

  • USDB: 現象論的な相互作用

  • NN-only: 先程の章で計算した２体力から導出された相互作用

using NuclearToolkit

target = "Mg24"
n_eigen=10;targetJ=[]                                                                                                        
res_usdb = main_sm("./usdb.snt",target,n_eigen,targetJ) 
res_nn  = main_sm("./vsimsrg_sd-shell_coreO16refO16_O16_hw20e4_Delta0.0.snt",target,n_eigen,targetJ)      
""

  Mg24    Z,N=(12,12)     c(8,8)     v(4,4)  mdim:        28503 (  4.45 ) 

J [0.0, 2.0, 2.0, 4.0, 3.0, 4.0, 0.0, 2.0, 5.0, 1.0]
En.   -87.1044   -85.6021   -82.9883   -82.7320   -82.0341   -81.2219   -79.7662   -79.6227   -79.3076   -79.2863 
Ex.     0.0000     1.5023     4.1161     4.3724     5.0704     5.8826     7.3383     7.4817     7.7969     7.8182 
  Mg24    Z,N=(12,12)     c(8,8)     v(4,4)  mdim:        28503 (  4.45 ) 

J [0.0, 2.0, 2.0, 3.0, 4.0, 4.0, 5.0, 1.0, 6.0, 2.0]
En.  -109.0654  -107.7170  -106.0557  -104.8003  -104.7485  -103.2378  -101.1769  -100.7040  -100.1376  -100.1193 
Ex.     0.0000     1.3484     3.0097     4.2651     4.3170     5.8276     7.8886     8.3615     8.9278     8.9461 

""

ここで用いている相互作用"vsimsrg..."は、上で導出した\(e_\mathrm{max}=4\)と非常に小さい計算で、\(e_\mathrm{max}\)や\(\hbar\omega\)に対して収束した結果を与えるものではないことに注意。

２体力レベルでも現象論的相互作用と(そこそこ)似通ったスペクトルが得られている。
binding energyについては、現象論的相互作用の場合は、コア(今の場合、\({}^{16}\mathrm{O}\))やCoulomb相互作用は現象論的に与えるのに対し、 VS-IMSRG法では、coreとvalence空間のdecouplingの際に、reference state(≒コア)のエネルギーも計算しているため、 バレンス核子が稼ぐエネルギーとあわせて勘定してやればよい。

3.6. 殻模型計算コード

コミュニティ内においては、古くからshell-model計算を行うコードが開発・公開されており、

などが(もちろん他にも)ある。2024年現在においても精力的に開発が行われているものとしては、清水則孝氏(現: 筑波大学 計算科学研究センター)によるKSHELLが、その機能の豊富さ・性能のいずれの面においても抜きん出ており、事実上これ一択、という状況にある。

筆者のNuclearToolkit.jlにもshell-model計算を行うためのコード群としてShellModel.jlというものを内部に含んでいるものの、これはKSHELLのような高度な機能は持たず、新しいアルゴリズムや代理モデルなどの開発用途に適したものになっている。 もう少し細かく言うと、KSHELLでは行列要素を保持せずon the flyで計算することでメモリの使用量を抑え、大規模な計算を可能としている一方でShellModel.jlでは行列要素(そのものではなく1b,2b-jumpと呼ばれる必要な遷移)をあらかじめ保持することが前提となっているため、大規模な計算には向いておらず、せいぜいラップトップ上で\(sd\)〜lower \(pf\) shellでKSHELLよりも高速に計算ができる程度である。

3.7. 参考文献&謝辞

  • Alex Brown, Lecture Note:
    shell-model計算に関するほぼ全ての必要な情報は、Alex Brown氏@MSUのLecture Noteにまとめられている。 Webで見つかりやすいものは2005年版だが、より新しいバージョンとして、 Nuclear Talent(スクール)用の2017年版資料がMorten Hjorth-Jensen氏@MSUのGitHubレポジトリ内で公開されている。

  • 計算力学レクチャーコース: 固有値計算と特異値計算(丸善出版):
    Lanczos法など行列の固有値計算や関連の話題については素晴らしい書籍が多数ある。筆者は実装の際にこちらの本を参考にさせて頂いた。

  • KSHELL code:
    NuclearToolkit.jlにおいても、Tick-Restart法やBlock-Lanczos法などのLanczos法の種々の拡張を実装しているが、 その開発段階においては、KSHELLの作者である清水則孝氏に多大なる助言を頂きながら、KSHELLのソースコードも参考にさせて頂いた。

前へ

2. 核子系の第一原理計算

次へ

4. Emulator/Surrogate model