ガウス過程（Gaussian Process）

6. ガウス過程（Gaussian Process）#

ガウス過程（Gaussian Process, GP）は、関数の分布を扱うベイズ的なモデルである。主に回帰、ベイズ最適化などで利用される。

特に以下では、関数の回帰を行う関数の分布を推定・生成する方法としての観点から解説する。

理論的な詳細等については下記のガウス過程の名著(通称: GPML)を参照されたい。著者のページから無償でPDFが入手可能である:
"Gaussian Processes for Machine Learning" by Carl Edward Rasmussen and Christopher K. I. Williams

6.1. 概要#

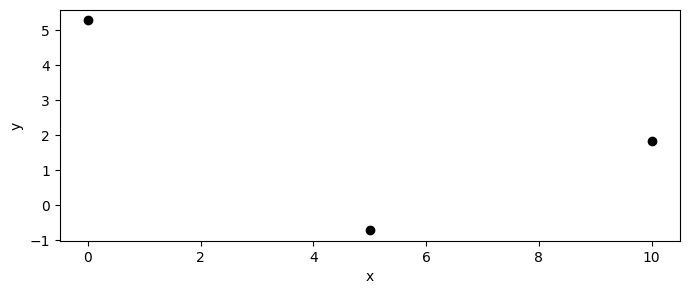
../_images/fb1984c68ee78a755e4fa62536b5e416ef4bd95225a60d3c12adf0b2feba04cd.png

今、図のようにデータが観測されているとする。このデータを説明する関数は無数に存在する。そんな中、単一の関数を選ぶのではなく、「もっともらしい」関数の分布を考えることができれば、より柔軟にデータを説明できると考えられる。

ガウス過程は、このような関数の分布を直接扱うための枠組みの１つである。背後にある考え方については、以下のとおりである。

任意の近傍二点に対して、その点での関数値は似ている(≒連続)であろう。
"似ている"度合いを非負の値を持つカーネル関数で定量化する。
既知のデータと未知の点での関数値の同時分布を考え、それが多変量ガウス分布に従うと仮定する。

とくに最後の点がガウス過程の名前の由来であると理解してもらってよい。

6.2. ガウス過程の定義#

観測データが \(\mathcal{D} = \{(x_i, y_i)\}_{i=1}^{n}\) で与えられるとする。ここで、\(x_i \in \mathbb{R}\) は説明変数、\(y_i \in \mathbb{R}\) は目的変数である。説明変数・関数値とも、多次元でも構わないが、ここでは単純化のために1次元としよう。

自分の興味のある\(m\)個の点 \(\mathbf{x}^* \) に対して、関数値 \(\mathbf{y}^*\) を予測したいとする。このときの\(\mathbf{x}^* = \{x_1^*, x_2^*, \ldots, x_m^*\}\) は、観測データ \(\mathcal{D}\) の説明変数 \(\mathbf{x}_i\) (データ点)とは異なる点であるとし、予測点とでも呼ぶことにする。

そのとき、\(\mathbf{x}, \mathbf{x}^*\) に対する関数値 \(\mathbf{y}, \mathbf{y}^*\) の同時分布が以下のように多変量ガウス分布に従うと仮定する。

\[\begin{split} \begin{pmatrix} \mathbf{y} \\ \mathbf{y}^* \end{pmatrix} \sim \mathcal{N} \left( \begin{pmatrix} \mu_\mathbf{x} \\ \mu_{\mathbf{x}^*} \end{pmatrix}, \begin{pmatrix} K(\mathbf{x}, \mathbf{x}) & K(\mathbf{x}, \mathbf{x}^*) \\ K(\mathbf{x}^*, \mathbf{x}) & K(\mathbf{x}^*, \mathbf{x}^*) \end{pmatrix} \right) \equiv \mathcal{N} \left( \boldsymbol{\mu}, \Sigma \right) \end{split}\]

平均ベクトルと共分散行列は、データ点と予測点を合わせて\(n+m\)次元のベクトル・行列としてまとめて書いた。予測点を考えるときは、描画点を多数用意することが多いため、\(m\)は大きな値になることも多い。

ひとたび多次元正規分布の平均ベクトルと共分散行列が与えられれば、条件付き分布もまた多次元正規分布になるため、以下のように、予測点での関数値の分布を得ることができる。

\[ p(\mathbf{y}^*|\mathbf{y}) = \mathcal{N}\left( \mu_{\mathbf{x}^*} + K(\mathbf{x}^*, \mathbf{x}) K(\mathbf{x}, \mathbf{x})^{-1} (\mathbf{y} - \mu_{\mathbf{x}}), K(\mathbf{x}^*, \mathbf{x}^*) - K(\mathbf{x}^*, \mathbf{x}) K(\mathbf{x}, \mathbf{x})^{-1} K(\mathbf{x}, \mathbf{x}^*) \right) \]

ここでは、多次元正規分布の条件付き確率分布の計算(3章)を用いた。この意味するところは、予測点での関数値 \(\mathbf{y}^*\) は、観測データ \(\mathcal{D}\) に基づいて平均と分散が決定される正規分布に従う、ということである。それぞれの予測点での関数値が分布に従うため、予測点での関数値の不確実性を考慮することができる。

6.3. カーネルとハイパーパラメータ#

カーネル関数 \(k(x, x')\) は、関数の滑らかさや周期性などの事前知識を反映する。代表的なカーネルは以下の通りである：

RBF（ガウス）カーネル:

\[ k(x, x') = \tau \exp\left(-\frac{(x-x')^2}{2l^2}\right) \]

ハイパーパラメータ：\(\tau\)（出力のスケール）、\(l\)（長さ尺度, 相関長:correlation lengthとも言う）
Matérnカーネル:

\[ k(x, x') = \tau \frac{2^{1-\nu}}{\Gamma(\nu)} \left( \sqrt{2\nu} \frac{|x-x'|}{l} \right)^\nu K_\nu \left( \sqrt{2\nu} \frac{|x-x'|}{l} \right) \]

ここで、\(K_\nu\) は第\(\nu\)種の変形ベッセル関数、\(\Gamma(\nu)\) はガンマ関数である。

ハイパーパラメータ：\(\tau\)（出力のスケール）、\(l\)（長さ尺度）、\(\nu\)（平滑度）

なかでも\(\nu=3/2\)や\(\nu=5/2\)がよく使われる。\(\nu=1/2\)のときは、指数カーネルとも呼ばれ、\(\nu \to \infty\)のときはRBFカーネルとなる。 RBFカーネルは無限回微分可能で非常に滑らかであるのに対し(それはデータが持つ連続性としては過剰な仮定と考えられ)、Matérnカーネルは\(\nu\)によって微分可能な回数が制御される。実用上においても、RBFカーネルで距離の近いデータ点を取りすぎると、数値的に不安定になることがある。

ハイパーパラメータは、対数尤度最大化などで推定されることが多い。上の、\(\tau, l\)をまとめて \(\theta = (\tau, l)\) と書くことにして、対数尤度の勾配は以下のように計算される。

\[ \frac{\partial}{\partial \theta_i} \log p(\mathbf{y}|\mathbf{x}, \theta) = \frac{1}{2} \mathbf{y}^\top K(\mathbf{x}, \mathbf{x})^{-1} \frac{\partial K(\mathbf{x}, \mathbf{x})}{\partial \theta_i} K(\mathbf{x}, \mathbf{x})^{-1} \mathbf{y} - \frac{1}{2} \mathrm{tr} \left(K(\mathbf{x}, \mathbf{x})^{-1} \frac{\partial K(\mathbf{x}, \mathbf{x})}{\partial \theta_i}\right) \]

また、カーネルが持つべき重要な性質としては、

対称性: \(k(x, x') = k(x', x)\)
正定値性: 任意の異なる点 \(\{x_1, x_2, \ldots, x_n\}\) に対して、対応するカーネル行列 \(K\) が正定値行列であること
非負性: \(k(x, x) \geq 0\) であること

が挙げられる。

問題

逆行列の微分と\(\log |\mathbf{A}|\)の微分の式(線形代数の章を参照)を用いて、上の対数尤度の微分に関する式を導出せよ。

6.4. ノイズの扱い#

ガウス過程では、観測データのノイズを自然に扱うことができる。

\[ y_i = f(x_i) + \epsilon_i, \quad \epsilon_i \sim \mathcal{N}(0, \sigma_n^2) \]

ここで、\(\epsilon_i\) は独立同分布に従うガウスノイズであるとする。このとき、観測データの関数値 \(\mathbf{y}\) の共分散行列は、以下のようにノイズの分散を加えたもの

\[ K(\mathbf{x}, \mathbf{x}) + \sigma_n^2 I \]

となる。ここで、\(I\) は単位行列である。このように、ノイズの分散を共分散行列に加えることで、ノイズを考慮した予測が可能となる。

一点注意すべきは、ノイズの分散 \(\sigma_n^2\) は、カーネルのハイパーパラメータとして推定されることが多いことである。既存のGPyなどのライブラリでは、データを与えた際に、ノイズの分散を含むハイパーパラメータを対数尤度最大化で推定する機能が備わっている。データは(多くの場合)標準化されていることが多いため、ノイズの分散は1よりもかなり小さい値になることが期待されるが、対数尤度最大化の結果、非常に大きな値になることがある。この場合、データが本来持つ不定性を過大評価してしまうため、予測が過度に平滑化されてしまうことがある。筆者の経験上、このあたりの問題を適切に理解した応用がなされていないものも多く散見するため、注意が必要である。

実装の背後にある理論や、データのドメイン知識が必要となる好例である。

6.5. 実装#

Pythonでは、GPyやscikit-learnなどのライブラリがガウス過程の実装を提供している。以下では、自前でMatérnカーネル(\(\nu=5/2\))を用いたガウス過程を実装してみる。

とりあえず、ハイパーパラメータを固定して、予測点での関数値の分布を計算してみよう。

Show code cell source

Hide code cell source

import numpy as np
import matplotlib.pyplot as plt
import copy
from scipy import special
from matplotlib.animation import FuncAnimation
from IPython.display import HTML


## ガウス過程のカーネル(共分散行列)の設計
def Mat52(Thetas,r):
    tau,sigma = Thetas
    thetar = r * np.sqrt(5.0)/sigma
    return tau * (1.0 + thetar + (thetar**2) /3.0) * np.exp(-thetar)

def KernelMat(Thetas,xt,xp):
    lt = len(xt); lp=len(xp)
    Ktt = np.zeros((lt,lt)); Kpt = np.zeros((lp,lt));  Kpp = np.zeros((lp,lp))
    for j in range(lt):
        for i in range(j,lt):
            r = abs(xt[i]-xt[j])
            tmp  = Mat52(Thetas,r) 
            Ktt[i,j] = tmp; Ktt[j,i] = tmp 
        for i in range(lp):
            r= abs(xp[i]-xt[j])
            Kpt[i,j] = Mat52(Thetas,r)
    for j in range(lp):
        for i in range(j,lp):
            r= abs(xp[i]-xp[j])
            tmp  = Mat52(Thetas,r)
            Kpp[i,j] = tmp; Kpp[j,i] = tmp
    return Ktt,Kpt,Kpp

## 事後共分散行列の計算
def calcSj(cLinv,Kpt,Kpp,yt,mu_yt,mu_yp):
    tKtp= np.dot(cLinv,Kpt.T)
    return mu_yp + np.dot(Kpt,np.dot(cLinv.T,np.dot(cLinv,yt-mu_yt))), Kpp - np.dot(tKtp.T,tKtp)

## Cholesky分解
def Mchole(tmpA,ln) :
    cLL = np.linalg.cholesky(tmpA)
    logLii=0.0
    for i in range(ln):
        logLii += np.log(cLL[i,i])
    return np.linalg.inv(cLL), 2.0*logLii

## データ点＆予測点の設定
np.random.seed(0)
x = np.linspace(2, 8, 10)
y = f(x)
y = (np.array(y) - np.mean(y)) / np.std(y)  # 標準化
xp = np.linspace(0, 10, 200)

## ガウス過程の実装
for Thetas in [[1.0, 0.5, 1e-1], [1.0, 1.0, 1e-2]]:
    lt=len(x); lp=len(xp)
    Ktt,Kpt,Kpp = KernelMat(Thetas[:2], x, xp)
 
    mu_yt= np.mean(y)*np.ones(lt)
    mu_yp= np.mean(y)*np.ones(lp)

    cLinv,logdetK = Mchole(Ktt,lt) 
    mujoint,Sjoint = calcSj(cLinv, Kpt, Kpp, y, mu_yt, mu_yp)
    sigmaj=[ Sjoint[j][j] for j in range(lp)]
    ysamples = [np.random.multivariate_normal(mujoint,Sjoint) for i in range(10)]

    fig = plt.figure(figsize=(8, 3))
    plt.scatter(x, y, color="k", label="data")
    plt.plot(xp, mujoint, color="b", label="mean")
    plt.fill_between(xp, mujoint-1.96*np.sqrt(sigmaj), mujoint+1.96*np.sqrt(sigmaj), color="b", alpha=0.2, label="95% CI")
    for ys in ysamples:
        plt.plot(xp, ys, alpha=0.3, linestyle="--")
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title(f"GP regression with Mat52 kernel (tau={Thetas[0]:6.2f}, sigma={Thetas[1]})")
    plt.legend()
    plt.show()
    plt.close()

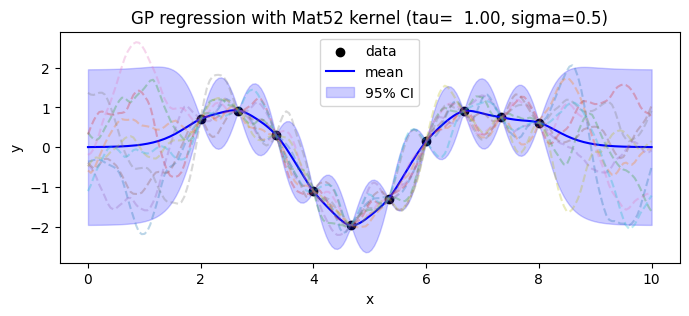
../_images/600c9ba899c4b229c02538502f1eff3fc848ae855f07300865000ef37226d421.png

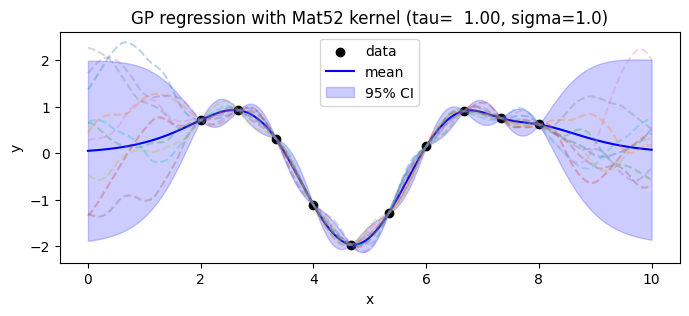
../_images/57d6e0e48569dd620bb544f660835d04373a992d1fb7bd3a1ced86a9465ff934.png

青線が、事後分布の平均、青色のバンドが、95%信頼区間を示している。破線で示したのは、事後確率から得られたサンプルである。

\(d\)個のデータ点と相関した\(m\)個の予測点を同時にサンプルすれば、各点で独立した値ではなく、連続的な関数のサンプルを得ることができる。

また\(K(\mathbf{x}, \mathbf{x})\)の逆行列を計算する際に、数値的に不安定になる。上の実装では、コレスキー分解を用いた。

\[ K(\mathbf{x}, \mathbf{x}) = LL^T \]

ここで、\(L\)は下三角行列である。これを用いると、逆行列の計算は以下のように安定に行うことができる。

\[ K(\mathbf{x}, \mathbf{x})^{-1} = (L^T)^{-1} L^{-1} \]

念の為、同じハイパーパラメータで、GPyのガウス過程の実装と比較してみよう。

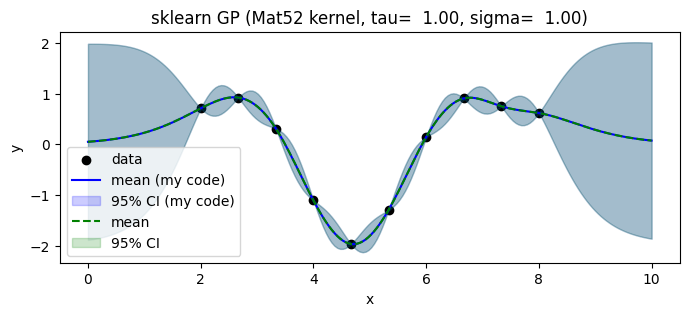
../_images/8544eea230ca032b08d8956c93ddb9dfe5c3937e9e59e0c2e287757b580bc6cc.png

両者がピッタリ重なっている事がわかる。ただし、GPyやscikit-learnなどのライブラリでは、データの分散や予測分散を別々にカスタマイズするのがやや面倒だったりもする。

6.6. \(\clubsuit\) 正規乱数の生成について#

余談になるが、正規分布に従う乱数の生成をどのように行えばよいだろうか？もちろんnumpyやscipyなどのライブラリを使えば簡単に生成できるが、どのように生成されているのか紹介しておこう。

簡単のため１次元の場合を考える。標準正規分布に従う乱数\(z\)を生成する方法の一つに、Box-Muller法がある。

Box-Muller法では、\(U_1, U_2\)を\([0,1)\)の一様分布に従う独立な乱数とするとき、以下の変換によって得られる\(Z_0, Z_1\)が標準正規分布に従うことを利用する。

\[\begin{split} \begin{align*} Z_0 & = \sqrt{-2 \ln U_1} \cos(2 \pi U_2)\\ Z_1 & = \sqrt{-2 \ln U_1} \sin(2 \pi U_2) \end{align*} \end{split}\]

この方法は、極座標変換を用いて、2次元の標準正規分布に従う乱数を生成し、それを1次元に分解している。半径部分が指数分布に、角度部分が一様分布に従うことを利用している。

コードで確かめてみよう。一様乱数を2つ生成し、Box-Muller法で標準正規乱数を生成し、散布図とヒストグラムを描画してみた。

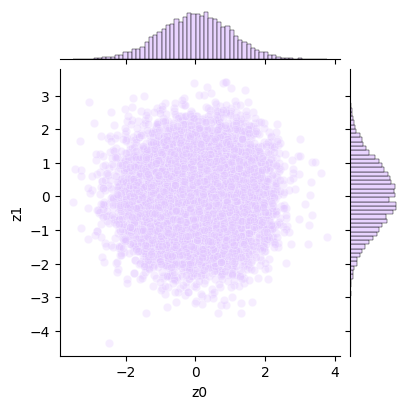
../_images/691ca8b2fb8b029ab584176033fe28ce8524db163bf67ff02d1eee27a39ffff3.png

続いて、多次元正規分布に従う乱数を生成する方法についても紹介しよう。こちらも、np.random.multivariate_normalなどの実装があるので、実用上はそれを使えばよいが、詳細な実現方法の一例を知っておくと便利である。多次元正規分布の乱数生成は、共分散行列 \(\Sigma\) のコレスキー分解を用いればよい。

\[ \Sigma = LL^T \]

このとき、標準正規分布に従う乱数ベクトル \(\mathbf{z} \sim \mathcal{N}(0, I)\) に対して、変換

\[ \mathbf{y} = L \mathbf{z} + \boldsymbol{\mu} \]

によって、\(\mathbf{y} \sim \mathcal{N}(\boldsymbol{\mu}, \Sigma)\) に従う乱数ベクトルを生成できる。

余談ついでに昔話をすると、Numpyの多次元正規分布は(少なくとも筆者が大学院生の頃は)何も考えずに使うとthread-unsafe、つまりマルチスレッド環境で使うと同様の乱数が生成されてしまう仕様であった。そのことに気がついたのは、粒子フィルタ(particle filter)と呼ばれる複数のworkerでサンプリングを行う、マルコフ連鎖モンテカルロ法の逐次バージョン的なアルゴリズムを実装していたときで、独立なはずのworkerが同じ乱択を繰り返していることに気が付いた。 Numpy 2.0になってからは、RNG(乱数生成器)周りでの改良が行われたようだが、やはり実際の乱数生成の結果を都度確認する癖はつけておいた方がよいだろう。

6.7. ベイズ最適化#

ガウス過程は、ベイズ最適化の核としても広く使われる。関数の振る舞いをガウス過程でモデル化し、その不確実性を考慮しながら最適化を進めていく。

とくに、１回の観測(や数値実験など)にコストがかかり、勾配が利用できないような関数の最適化に有効である。また、探索と活用のトレードオフを考慮しながら、効率的に最適解に近づくことができることも多く機械学習のハイパーパラメータチューニングなどにも利用される。探索というのは「井の中の蛙状態が怖いので、未知の領域を探索してみよう」というイメージで、活用というのは「今までの経験から良さそうなところを掘り下げてみよう」というイメージである。

例えば今の関数の振る舞いを、パラメータ空間に対するコスト関数だと考え、その最小化や最大化を目指すとする。すでに得られているデータ点をもとに、次に評価する点を獲得関数で決定する。言い換えると、情報利得が高そうかつ、良さそうな点を次に評価するための、戦略を立てるための枠組みとも言える。

以下に、実装例を示す。なお、獲得関数には、期待改善量(Expected Improvement, EI)を用いている。

\[ EI(x) = (\mu(x) - y_\mathrm{best}) \Phi(z) + \sigma(x) \phi(z), \quad z = \frac{\mu(x) - y_\mathrm{best}}{\sigma(x)} \]

ここで\(\Phi, \phi\)はそれぞれ標準正規分布の累積分布関数と確率密度関数である。この他にも

PI（Probability of Improvement): 現状の最適値よりもさらに良くなる確率を計算して次点を選ぶ方法
UCB（Upper Confidence Bound)/LCB（Lower Confidence Bound): ガウス過程の予測平均と分散を組み合わせて次点を選ぶ方法