線形回帰

5. 線形回帰#

この章では、前章の単回帰を拡張した線形回帰について解説する。

最も単純な線形回帰は、以下の多項式回帰である。

定義: 多項式回帰

回帰曲線を、多項式の重み付き和で表現する回帰を 多項式回帰(polynomial regression) と呼ぶ。

\[ y(x, \boldsymbol{w}) = w_0 + w_1 x + w_2 x^2 + \cdots + w_p x^p = \sum_{j=0}^p w_j x^j \]

ここで、\(x\)は入力変数、\(y\)は出力変数、\(w\)はパラメータベクトル、\(p\)は多項式の次数である。

線形回帰(Linear Regression)はしばし、この多項式回帰を指すこともあるが、 より一般には、基底関数と呼ばれる関数を用いた定義となる:

定義: 線形回帰

\[ y(x,{\bf w})= \sum^{M-1}_{j=0} w_j \phi_j(x) = {\bf w}^T\boldsymbol{\phi}(x) \]

ここで、\(\boldsymbol{\phi}(x)\)は基底関数と呼ばれる。 "線形"の意味するところは、基底関数の形状が線形であることではなく、基底関数を重ね合わせるパラメータ(重み)\(\boldsymbol{w}\)それぞれについて、1次式で表されることを指す。

上記の基底関数としては、ガウス型基底関数、シグモイド基底関数、スプライン基底関数、フーリエ基底関数などがある。 「幾つかの関数を重みをつけて重ね合わせることで、データをうまく表現するような柔軟な関数を作る」 というイメージを持つと良い。

5.1. 線形回帰の一般的な性質#

線形回帰モデル:\(y(x,{\bf w})= \sum^{M-1}_{j=0} w_j \phi_j(x) = {\bf w}^T\boldsymbol{\phi}(x)\)を考える。

ここで\(\boldsymbol{\phi}(x)\)は基底関数のベクトルで、\(p\)次の多項式回帰の場合は\(\boldsymbol{\phi}(x)=(1, x, x^2, \ldots, x^p)^T\)となる。実際に、ベクトルの内積の形で書き下すと\({\bf w}^T\boldsymbol{\phi}(x)=w_0 + w_1x+ w_2x^2+ \cdots + w_{p}x^p\)となり、\(p\)次多項式の出力を与えることがわかる。

さて目標変数\(t_i\) (あるいは観測値)が、\(y(x_i,{\bf w})\)と平均0、精度\(\beta\equiv 1/\sigma^2\)の誤差\(\epsilon_i\)の和: \(t_i=y(x_i,{\bf w})+\epsilon_i\)で与えられていると仮定する。 つまり、\(t\)の確率分布が\(p(t|x,{\bf w},\beta) = \mathcal{N}(t|y(x,{\bf w}),\beta^{-1})\)で与えられるとする。

いまデータ点が\(D\)個あるとする。入力\(\boldsymbol{\mathrm{X}}=\{x_1, x_2, \ldots, x_D\}\)と、対応する目標値を\(\boldsymbol{\mathrm{t}}=\{t_1,t_2,\ldots, t_D\}\)と表すことにしておこう。

これらのデータ点が上の分布\(p(t|x,{\bf w},\beta)\)から独立に生成されたと仮定すると、データの目標変数についての確率分布は

\[ p(\boldsymbol{\mathrm{t}}|\boldsymbol{\mathrm{X}},{\bf w},\beta) = \prod^D_{n=1} \mathcal{N}(t_n|{\bf w}^T \boldsymbol{\phi}(x_n) ,\beta^{-1}) \]

で与えられる。つまり、(少々くどいが)\(t\)の各点が\(y(x,{\bf w})\)の周りに、精度\(\beta\)のガウス分布でばらついているということである。

(以下では、確率分布の条件部分にある\(x\)などを適宜省略する)このとき、対数尤度と呼ばれる量は

\[ \ln p(\boldsymbol{\mathrm{t}}|{\bf w},\beta) = \sum^D_{n=1} \ln \mathcal{N}(t_n|{\bf w}^T\boldsymbol{\phi}(x_n), \beta^{-1}) = \frac{D}{2}\ln\beta - \frac{D}{2}\ln(2\pi) -\beta E_D({\bf w}) \]

となる。なお、\(\phi(x_n)\)は点\(x_n\)における基底関数値を並べた\(M\)次元のベクトルで、\(E_D\)は二乗和誤差:

\[ E_D({\bf w}) \equiv \frac{1}{2}\sum^D_{n=1} \left( t_n- {\bf w}^T \boldsymbol{\phi}( x_n) \right)^2 \]

で、前の2つの項はモデルパラメータ\({\bf w}\)に依存しないことから、対数尤度の最大化が、二乗和誤差の最小化と等価であることがわかる。

対数尤度の勾配を書き下し、勾配を用いて対数尤度の最大化(最尤推定と呼ぶ)を考えよう。つまり

\[ \nabla_\mathbf{w} \ln p(\boldsymbol{\mathrm{t}}|{\bf w},\beta) = \beta \sum^D_{n=1} \left( t_n -{\bf w}^T \boldsymbol{\phi}(x_n) \right) \boldsymbol{\phi}(x_n) =0 \]

の(p次元ベクトルに対する)方程式の根を求めてやれば良い。

上の式を変形すると

\[ \sum^D_{n=1} t_n \boldsymbol{\phi}(x_n) = \sum^D_{n=1} ({\bf w}^T \boldsymbol{\phi}(x_n)) \boldsymbol{\phi}(x_n) \]

となり、これを\({\bf w}\)について解くことで、

\[ {\bf w} = ( \boldsymbol{\Phi}^T\boldsymbol{\Phi} )^{-1} \boldsymbol{\Phi}^T \boldsymbol{t} \]

が根であることがわかる。 ここで、\(\boldsymbol{t}\)は目標値ベクトルで、\(\boldsymbol{t}=(t_1, t_2, \ldots, t_D)^T\)で与えられる。 また、\(\boldsymbol{\Phi}\)は計画行列(Design Matrix)と呼ばれ、\(\boldsymbol{\Phi}_{nj} = \phi_j(x_n)\)で与えられる。顕に書くと...

\[\begin{split} \boldsymbol{\Phi} = \begin{pmatrix} \phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_{M}(x_1) \\ \phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_{M}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ \phi_1(x_D) & \phi_2(x_D) & \cdots & \phi_{M}(x_D) \\ \end{pmatrix} = \begin{pmatrix} \boldsymbol{\phi}(x_1)^T \\ \boldsymbol{\phi}(x_2)^T \\ \vdots \\ \boldsymbol{\phi}(x_D)^T \\ \end{pmatrix} \end{split}\]

多項式回帰の場合は

\[\begin{split} \boldsymbol{\Phi} = \begin{pmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^p \\ 1 & x_2 & x_2^2 & \cdots & x_2^p \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_D & x_D^2 & \cdots & x_D^p \\ \end{pmatrix} \end{split}\]

つまり、最尤推定を与えるパラメータ\({\bf w}_{ML}\)は、観測値ベクトル\(\boldsymbol{t}\)と計画行列\(\boldsymbol{\Phi}\)を用いて閉じた形で与えられる。 別の言い方をすると、\(\boldsymbol{w}\)の値を少しずつ変えて対数尤度を最大化するような反復計算を行う必要がなく、ベクトル・行列の演算だけで最尤推定が求まる。この点が最も重要である。 なお、ここでは暗黙のうちに、\(\boldsymbol{\Phi}^T\boldsymbol{\Phi}\)の逆行列が数値的に安定に計算できることを仮定している。

ちなみに...上ではわざわざ観測値が予測値の周りに精度\(\beta\)のガウス分布でばらついていると仮定したが、実際にはこの仮定は、上記の最尤推定の結果を導くためには必要ない。 後のベイズ線形回帰の導入のために便宜上この仮定を置いた。混乱した人のために、\(\beta\)を省いた形での議論を再度整理しておこう:

  1. 下記のようなデータ点\(D\)個が与えられたとする:

    \[ \{(x_1,t_1), (x_2,t_2), \ldots, (x_D,t_D)\} \]

  2. これらのデータ点を、基底関数\(\boldsymbol{\phi}(x)\)を用いた線形回帰モデル\(y(x,{\bf w})={\bf w}^T \boldsymbol{\phi}(x)\)で表現したいとする。

  3. このとき、\(\boldsymbol{w}\)を、二乗誤差を最小化するように決定したい。

    \[ E_D({\bf w}) = \frac{1}{2}\sum^D_{n=1} \left( t_n- {\bf w}^T \boldsymbol{\phi}( x_n) \right)^2 \]

  4. 二乗誤差をパラメータで微分し、勾配が0となる点を求める。

    \[ \nabla_\mathbf{w} E_D({\bf w}) = - \sum^D_{n=1} \left( t_n -{\bf w}^T \boldsymbol{\phi}(x_n) \right) \boldsymbol{\phi}(x_n) =0 \]

    このとき、二乗誤差の定義に\(1/2\)や\(1/D\)、\(\beta\)などの定数をかけても、勾配が0となる点は変わらないことに注意。

  5. 上の式を変形し、\({\bf w}\)について解くと、最尤推定を与えるパラメータ\({\bf w}_{ML}\)が得られる。

    \[ {\bf w}_{ML} = ( \boldsymbol{\Phi}^T\boldsymbol{\Phi} )^{-1} \boldsymbol{\Phi}^T \boldsymbol{t} \]

上の式を用いて、最尤推定を与えるパラメータ\({\bf w}_{ML}\)を求める関数を実装してみよう。

次の１次元擬似データの回帰を考えてみる。

Hide code cell source 
import numpy as np
from matplotlib import pyplot as plt

## データ点の生成
np.random.seed(1234)
x = np.linspace(-2.0, 6.0,1000)
beta = 1.e+2
xt = np.linspace(0.0,4.0,20)
yt = np.sin(xt) + np.array([ np.random.normal(0.0,1.0/np.sqrt(beta)) for i in range(len(xt))])

fig = plt.figure(figsize = (10,3))
axs = [fig.add_subplot(111)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].set_xlabel("x")
axs[0].set_ylabel("y")
axs[0].legend()
plt.show()
plt.close()
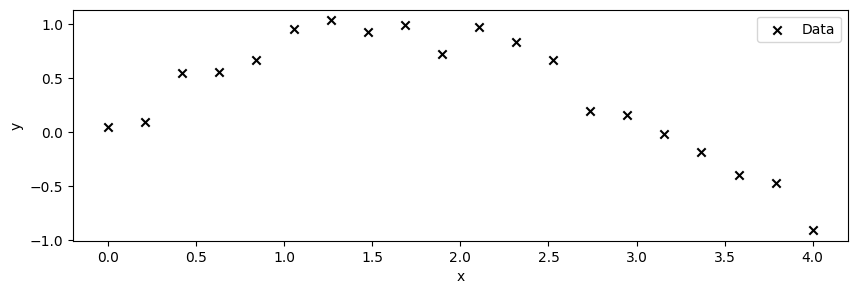
../_images/90f05e67783bc720d14fe142cf3283bb4725297f59dc41ab9c252544905d3841.png

これを,numpyモジュールの多項式fit関数と、上の計画行列によって3次式で回帰してみると...

Hide code cell source 
N = len(xt)

##　多項式の次元を固定しておく
p=3

##numpyのfit
yp = np.poly1d(np.polyfit(xt, yt, p))(x) 

## 計画行列を用いる方法
def phi(x,p):
    return np.array([ x**i for i in range(p+1)])
Phi = np.zeros((N,p+1))
for i in range(N):
    xn = xt[i]
    tmp = phi(xn,p) 
    for j in range(p+1):
        Phi[i][j] = tmp[j]
S = np.linalg.inv(np.dot(Phi.T,Phi))
wML = np.dot(S,np.dot(Phi.T,yt))
yD = [ np.dot(wML,phi(xn,p)) for xn in x ]

#図のplot
fig = plt.figure(figsize = (13,4))
axs = [fig.add_subplot(121),fig.add_subplot(122)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].plot(x,yp,label="np.polyfit",color="r",alpha=0.5)
axs[0].plot(x,yD,label="DMat",linestyle="dotted", color="g")
axs[0].set_xlabel("x")
axs[0].set_ylabel("y")
axs[0].legend()

axs[1].plot(x,np.log10(abs(yp-yD)))
axs[1].set_xlabel("x")
axs[1].set_ylabel("log10|y_np - y_DMat|")
plt.show()
plt.close()
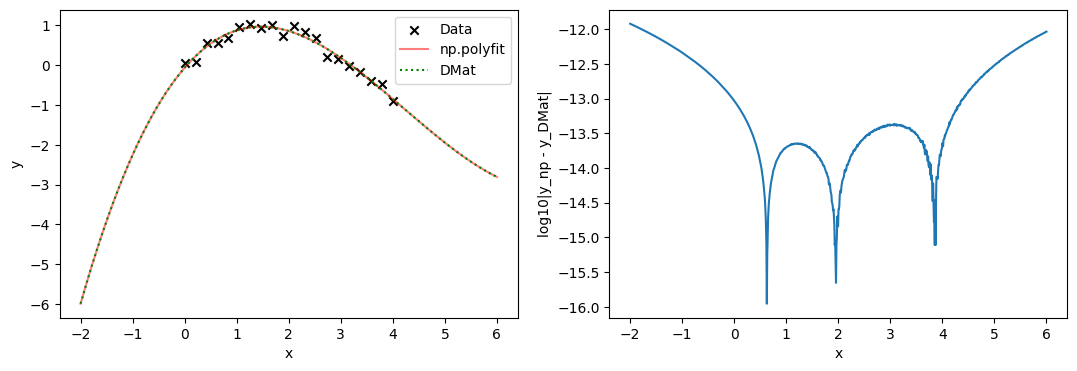
../_images/73643efe694b152c17231e18ae6c7efda098c8f946ea5d0cae762fcc706729c5.png

となり、ライブラリの出力と計画行列を用いた最尤推定の結果とがピッタリ(ざっくり14桁程度)一致していることがわかる。

5.1.1. \(\clubsuit\) L2正則化項がある場合への拡張#

詳しくはニューラルネットワークや正則化の章で解説するが、一般に回帰問題においては、与えられたデータに対する過度な適合(過適合)とそれによる汎化性能(予測性能)の低下を防ぐために、正則化と呼ばれる手法が用いられる。今の場合も、データは背後にある関数にノイズを足して生成されているが、そのノイズを含んだデータに対して、完全に適合するようなモデルを作ると、ノイズまで含んだ関数を作ってしまうことになる。これは多くの場合、望ましくない。

正則化とは、モデルの複雑さを制限することで、過適合を防ぐ手法である。 なかでも、L2正則化は、パラメータの二乗和を小さくするように、最尤推定を行う手法であり、機械学習を始めとする多くの分野で用いられている。

今まで、モデルとなる関数の良さを測る際は、二乗和誤差関数を用いていたが、これにL2正則化項と呼ばれる重みの二乗和を加えたものを用いる。

\[ \mathcal{L}(\mathbf{w}, \lambda) \equiv \frac{1}{2}\sum^N_{n=1} \left( t_n- {\bf w}^T \boldsymbol{\phi}(x_n) \right)^2 + \frac{\lambda}{2} {\bf w}^T{\bf w} \]

第二項がL2正則化項で、重みが大きければ大きいほど、対数尤度が小さく(誤差関数\(\mathcal{L}\)の値が大きく)なってしまうような尺度になっていることがわかる。 ここで、\(\lambda\)は正則化の強さを決めるパラメータで、\(\lambda\)が大きいほど、正則化の制限の強さが増す。

この式について、上と同様に勾配を計算し、しばらく計算してやると、最尤推定を与えるパラメータ\({\bf w}\)は

\[ {\bf w}_{ML,L2} = (\lambda I + \boldsymbol{\Phi}^T\boldsymbol{\Phi} )^{-1} \boldsymbol{\Phi}^T \boldsymbol{\mathrm{t}} \]

となり、計画行列に\(\lambda \times\)(単位行列)を足した形となる。

対数尤度が\(|w|^2\)に比例することから実はほとんど自明なのだが、あとで示すように「L2正則化を課すこと」は、 「パラメータの事前分布にガウス分布を仮定すること」と等価である。

5.1.2. データの規模に関する注意点#

上では、線形回帰の最適なパラメータは閉じた形で求められることを紹介した。

これは、最適解を得る指針が明確であるというメリットの反面、データのサイズが大きくなるにつれてデメリットが生じる。

まずデータ数\(N\)が大きくなれば、数値計算上のボトルネックは行列に対する演算となる。 例えば\(N=10^6\)とすると、正方行列の行列要素を倍精度(Float64)の浮動小数点で保持しようとすると、 変数だけで\((10^6)^2 \times 8 = 8 \times 10^{12}\)バイトとなり、約8TBとなる。 これは、明らかに一般的なPCのメモリや記憶容量のサイズを超えている。

また、一般に主要な行列演算は、計算量が\(O(N^2)\)や\(O(N^3)\)となるため、データ数が大きくなると、計算量が膨大になり現実的な時間で計算が終わらなくなる。

このような理由から、データ数が大きくなると、線形回帰のような閉じた形で解けるモデルでも、 逐次パラメータを更新し、最適解を探索するような手法が必要となる。

機械学習のパラメータ最適化などは、このような逐次的な手法が用いられることが多く、詳しくは後の章で説明する。

5.2. \(\clubsuit\) ベイズ線形回帰#

次に、パラメータ\({\bf w}\)をベイズ的に取り扱う事を考える。 このノートでいう"ベイズ的"とはせいぜい「パラメータを点推定する立場より有限の幅をもつ確率分布としてパラメータを考える」という程度の意味である。

パラメータ\({\bf w}\)が、平均\(\boldsymbol{\mu}_w\),共分散\(\boldsymbol{\Sigma}_w\)で指定される多次元の正規分布に従うと仮定する:

\[ {\bf w} \sim \mathcal{N}(\boldsymbol{\mu}_w,\boldsymbol{\Sigma}_w) \]

このとき、データ点\(t\)が観測されたときのパラメータの事後分布は\(p({\bf w}|\boldsymbol{\mathcal{t}}) = \mathcal{N}(\tilde{\boldsymbol{\mu}},\tilde{\boldsymbol{\Sigma}})\)で与えられる。

ここで事後分布の平均および共分散は以下のとおりである:

\[\begin{split} \begin{align*} \tilde{\boldsymbol{\Sigma}}^{-1} & =\boldsymbol{\Sigma}^{-1}+\beta\boldsymbol{\Phi}^T \boldsymbol{\Phi}, \\ \tilde{\boldsymbol{\mu} } & = \tilde{\boldsymbol{\Sigma}} (\boldsymbol{\Sigma}^{-1} \boldsymbol{\mu} + \beta \boldsymbol{\Phi}^T \boldsymbol{\mathcal{t}}) \end{align*} \end{split}\]

この式の導出は、3章末尾に紹介した、多次元正規分布のベイズの定理の節にある式を用いれば良い。 具体的には、観測点\(\boldsymbol{t}\)が、\(\boldsymbol{w}\)に条件付けられた多次元正規分布に従うことと、

\[ p(\boldsymbol{\mathrm{t}}|\boldsymbol{w}) = \mathcal{N}(\boldsymbol{\mathrm{t}}|\boldsymbol{\Phi} \boldsymbol{w}, \beta^{-1} I) \]

下記の式(３章)を見比べてやればよい。

\[\begin{split} \begin{align*} p(\mathbf{x}) &= \mathcal{N}(\mathbf{x}| \boldsymbol{\mu}, \Lambda^{-1}) \\ p(\mathbf{y} | \mathbf{x}) &= \mathcal{N}(\mathbf{y}| A \mathbf{x} + \mathbf{b}, L^{-1}) \end{align*} \end{split}\]

いま

\[\begin{split} \begin{align*} \mathbf{x} & \rightarrow \boldsymbol{w}, \\ \mathbf{y} & \rightarrow \boldsymbol{t}, \\ \boldsymbol{\mu} & \rightarrow \boldsymbol{\mu}_w, \\ \Lambda & \rightarrow \boldsymbol{\Sigma}_w^{-1}, \\ A & \rightarrow \boldsymbol{\Phi}, \\ \mathbf{b} & \rightarrow 0, \\ L & \rightarrow \beta I \end{align*} \end{split}\]

と対応させれば良い。

ここで簡単のため事前分布をさらに簡略化しよう。 事前分布の平均\(\boldsymbol{\mu}_w\)が\(0\)(ベクトル)かつ、パラメータの事前分布の共分散が対角的(独立な分散をもつ)でなおかつ値が同じ,つまり、上の\(\boldsymbol{\Sigma}_w=\alpha^{-1}I\)とかける場合を考える。

このとき、事後分布の平均および共分散は以下のように簡略化される:

\[\begin{split} \begin{align*} \tilde{\boldsymbol{\Sigma}}^{-1} &= \alpha I +\beta\boldsymbol{\Phi}^T \boldsymbol{\Phi} \\ \tilde{\boldsymbol{\mu}} & = \beta \tilde{\boldsymbol{\Sigma}} \boldsymbol{\Phi}^T \boldsymbol{t} \end{align*} \end{split}\]

この条件のもとで 対数事後確率(log posterior) と呼ばれる量は、対数尤度と対数事前分布の和として、

\[ \ln p({\bf w}|\boldsymbol{\mathrm{t}}) = -\frac{\beta}{2}\sum^N_{n=1} \left(t_n - {\bf w}^T \phi(x_n) \right)^2 -\frac{\alpha}{2} {\bf w}^T{\bf w} + \text{const.} \]

となる。

右辺の2項は、二乗誤差とL2正則化項に対応していることがわかる(最後の項は定数なので最大化/最小化とは関係ない)。したがって、正規分布で与えられる事前分布のもとでパラメータ\({\bf w}\)の事後分布を最大化すること、言い換えると観測値を考慮に入れた事後分布の平均・共分散行列の推定は、L2正則化項がある場合の誤差関数の最小化と等価であることがわかる。

実用上は\({\bf w}\)の分布を考えたあと、それを予測値の分布として伝播させる必要がある。 一般に予測分布を評価する際は、サンプリング法などが必要になるが、ガウス分布などの性質の良い確率分布を用いる場合は、事後分布が閉じた形で書き下すことができる(今の場合、ガウス分布となる)ため、事後分布に従う乱数などの生成は比較的容易となる。

未知の点\(x^*\)での値を\(t^*\)と書くことにすると、

\[ p(t^*|\boldsymbol{\mathrm{t}},\alpha,\beta) = \int p(t|{\bf w},\beta) p({\bf w}|\boldsymbol{\mathrm{t}},\alpha,\beta) d{\bf w} \]

今の場合、ガウス分布の性質から、予測分布は以下で与えられる

\[ p(t^*|x,\boldsymbol{\mathrm{t}},\alpha,\beta) = \mathcal{N}(t^*|\tilde{\boldsymbol{\mu}}^T\boldsymbol{\phi}(x),\sigma^2_N(x)) \]

ここで、予測分布の分散は

\[ \sigma^2_N(x)= \frac{1}{\beta}+\boldsymbol{\phi}(x)^T \tilde{\boldsymbol{\Sigma}}\boldsymbol{\phi}(x) \]
Hide code cell source 
## alpha(事前分布の精度=分散の逆数)は決め打ちとする
alpha = 1.e-5 #精度が小さい=分散が大きい=パラメータの事前知識が"弱い"

## wの事後分布の計算
I = np.diag([1.0 for i in range(p+1)])
Sigma = np.linalg.inv( alpha * I + beta * np.dot(Phi.T, Phi) )
mu = beta * np.dot(Sigma, np.dot(Phi.T,yt))

## 予測値(その分散)のリストを作成
y_BLR = []
for tx in x :
    tmp = phi(tx,p)
    mu_p = np.dot(mu,tmp)    
    term1 = 1.0/beta
    term2 =  np.dot(tmp,np.dot(Sigma,tmp))
    sigma_p = term1 + term2 
    #print("term1", term1, "term2", term2)
    y_BLR += [ [mu_p, sigma_p] ]
y_BLR = np.array(y_BLR).T

## plot
fig = plt.figure(figsize = (10,4))
axs = [fig.add_subplot(111)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].plot(x,yD,label="Maximum Likelihood",linestyle="dotted", color="red")
axs[0].plot(x,y_BLR[0],label="Mean",linestyle="dashed", color="blue")
axs[0].fill_between(x,y_BLR[0]+np.sqrt(y_BLR[1]),y_BLR[0]-np.sqrt(y_BLR[1]),label="1sigma", color="blue",alpha=0.5)
axs[0].fill_between(x,y_BLR[0]+3*np.sqrt(y_BLR[1]),y_BLR[0]-3*np.sqrt(y_BLR[1]),label="3sigma", color="gray",alpha=0.3)
axs[0].legend()
plt.show()
plt.close()
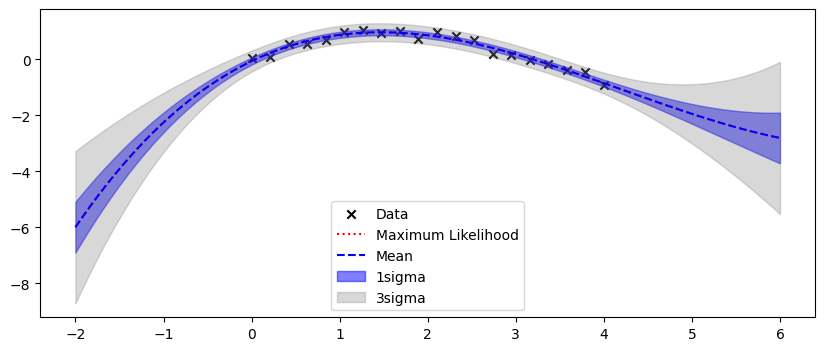
../_images/628d0a2150ec70313f1b0cd9ecbf46c792d7559954676d5949bb7c5c1d2ee79c.png

パラメータの広がりが予測に伝搬され、データが無いところで予測が不確かになっていることが見て取れる。

注) 上では、データの精度\(\beta\)(分散の逆数)や、パラメータ\({\bf w}\)の事前分布の精度\(\alpha\)を既知としたが、実際には、\(\beta\)そのものがわからなかったり、\(\alpha\)についての事前情報がない場合もある。

5.3. 学習の振り返りのためのチェックリスト#

▢ 　多項式回帰を説明できる
▢ 　線形回帰を説明できる
▢ 　線形回帰のパラメータの最尤推定の式を導出できる

目次