8. Eigenvector continuation (Emulator/Surrogate model)

代理モデルの構築は、(他の分野と同様)原子核物理における喫緊の課題である。

原子核物理(とくに理論計算)においては、2010年代になりようやく不定性評価の重要性が認識されるようになり、ベイズ推定などを用いた不定性評価が行われるようになった。 当然ながら、不定性評価を行うためには、計算コストが高い計算を何度も行う(サンプリングする)必要があり、 Full-CI法やPost-HF法などのhigh-fidelityな計算を繰り返し行うことは殆どの場合、現実的ではない。

そこで重要なのが、代理モデルの構築である。 代理モデルは分野によって呼び方は様々だが、emulatorやsurrogate modelなどと呼ばれるのが一般的で、 もう少しクラスを限定して、Reduced order modelやReduced basis modelなどとも呼ばれたりする。

この資料では、核子多体系の構造・反応計算に対して、計算コストを抑えつつ同等の(あるいは数%未満の誤差を許容した)結果を得る方法を ざっくばらんに代理モデルと呼ぶことにする。

8.1. 核子系多体問題の代理モデルを取り巻く動向

原子核物理学において代理モデルが大きく注目をあびるようになったのは、やはり下記の論文が契機と思われる: Eigenvector Continuation with Subspace Learning: D. Frame et al., Phys. Rev. Lett. 121, 032501 (2018)

この論文では、3次元のBose-Hubbard模型及びneutron matterの量子モンテカルロ計算についてEigenvector Continuation(EC)法と呼ばれる方法を用いて、パラメータを幾つか変更して実施した数点の計算結果から、所与のパラメータ点における波動関数やエネルギーを予測する方法を提案したものである。

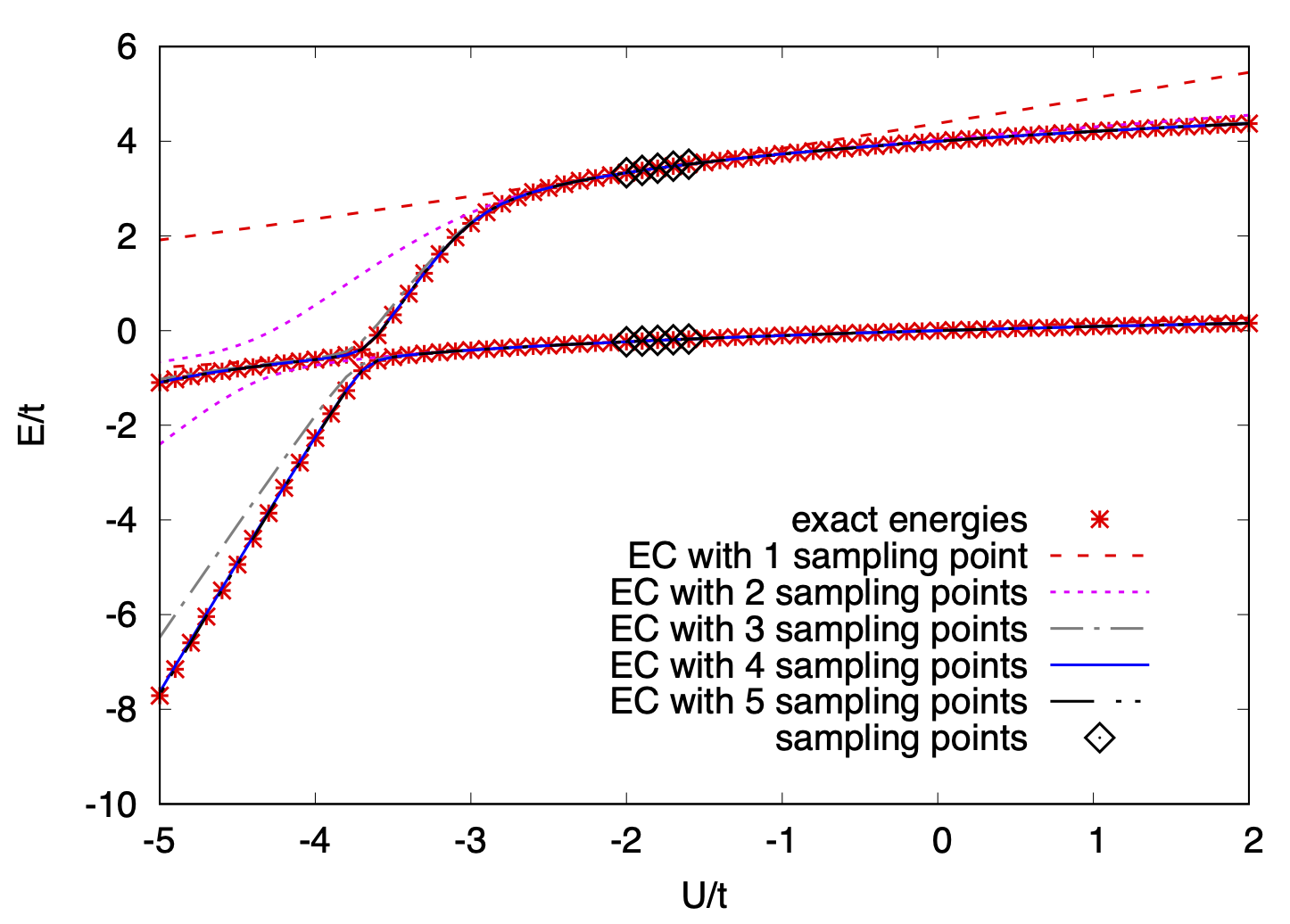
上に示したのは、上記の論文で示された、３次元Bose-Hubbard模型における基底状態と励起状態のエネルギーを、ポテンシャル項\(U\)とホッピング項\(t\)の比に対してプロットした図である。 図中の米?印は厳密解を示し、各線はEC法による予測値を示している。 線の違いは、ひし形で示されているサンプル点の数を示していて、 例えば異なる(最大たったの５点)パラメータ点で得られた２状態の波動関数の情報から、 他の任意のパラメータ点における波動関数を非常に精度良く予測(しかも外挿)できることが示されている。

上記の論文はその後、爆発的に引用され、とくに原子核物理の理論計算コミュニティで、 筆者を含めて構造計算、反応計算の両方において代理モデルの構築が一挙に進む契機となった。

その実、背景にある数学としては特段新しいものではなく、計算物理や応用数学の本に載っている(こともある)Rayleigh-Ritz法や、 Reduced basis methodとして他分野で理解されてきた手法の一種、あるいは再発明とみなすことができる。 とはいえ、例えば、流体力学の文脈で提唱された動的モード分解についても、内部で行う数学的な操作は特異値分解など既知の手法であるが、その提案は2008年であり、歴史は浅い。ある分野で既知とされるような概念でも、他分野で革新的になりえる好例とも言える。

その後、EC法は原子核物理コミュニティにおいても、Reduced basis methodsというより広い文脈から理解されるようになり、関連する研究が進められている。最近の動向としては、レビュー論文T.Duguet et al., Rev. Mod. Phys. 96, 031002 (2024)が詳しい。

8.2. Eigenvector Continuation (EC)

ここでは、具体的な問題を挙げることなく、EC法の概要を説明する。 興味のある系のHamiltonianを\(H(c)\)とすると、当然そのSchrödinger方程式は以下のようになる:

\[ H(c) | \psi(c) \rangle = E(c) | \psi(c) \rangle \]

ここで、\(c\)はパラメータである。例えば、\(c\)は上のホッピング項vsポテンシャル項の係数比であるとか、カイラル核力のLow-Energy Constantであるとかをイメージするとよい。

EC法では、この元々の問題をすでに数点解いた結果を用いて、所与のパラメータ点\(c_\odot\)での固有値・固有ベクトルを予測することを考える。 サンプル(ないしsnapshot)の数を\(N_s\)とすると、

\[\begin{split} \begin{align} H(c_1) | \psi(c_1) \rangle & = E(c_1) | \psi(c_1) \rangle \nonumber \\ & \vdots \nonumber \\ H(c_{N_s}) | \psi(c_{N_s}) \rangle & = E(c_{N_s}) | \psi(c_{N_s}) \rangle \nonumber \end{align} \end{split}\]

のそれぞれの波動関数により、\(N_s\)次元の空間を張るベクトルを作ることができる。 この\(N_s\)点のサンプル固有ベクトルを用いて、所与のパラメータの値における固有値問題を近似的に解くには、 以下の一般化固有値問題を考えることになる:

\[ \tilde{H}(c_\odot) \vec{v} = \lambda N \vec{v} \]

ここで、\(\vec{v}\)は\(N_s\)次元のベクトルであり、\(\tilde{H},N\)は\(N_s\)次元の行列で、それぞれ射影空間での\(H(c_\odot)\)の期待値と、サンプル波動関数同士の内積を要素とする行列である。

\[\begin{split} \begin{align} \tilde{H}_{ij} & = \langle \psi(c_i) | H(c_\odot) | \psi(c_j) \rangle \nonumber \\ N_{ij} & = \langle \psi(c_i) | \psi(c_j) \rangle \nonumber \end{align} \end{split}\]

このとき、\(\lambda\)は\(\tilde{H}(c_\odot)\)の固有値の近似値を与え、近似固有ベクトルは

\[ | \psi(c_\odot) \rangle \approx \sum_{i=1}^{N_s} v_i | \psi(c_i) \rangle \]

として与えられる。

このことから、一度サンプル波動関数を得てしまえば、別のパラメータ点で解くべき問題が、元の問題の次元ではなくサンプル数の次元にサイズダウンすることがわかる。 肝心なのは、そうして得られた波動関数がどれほどの精度で元の問題の波動関数を再現できるか、ということであるが、 (問題にもよるが)十程度のサンプル点をえることで、数%以下の誤差で波動関数を再現できることがFull-CI/valence-CI法やCoupled-Cluster法などの計算で報告されている。

なぜこのようなことができるのか、単純化して説明すると、いま考えているHamiltonianのもとで固有値ベクトルは、 naiiveには、サンプル点で得た固有ベクトルが張る低次元空間に十分近いことが予想されるためである。 なぜなら、Hamiltonianにはある程度の対称性や連続性があるため、現実的なパラメータ領域においては、 既に得たサンプルが貼る低次元空間における(一般化)固有ベクトルは、元の問題の波動関数と近いものであると期待される。

実際、EC法は相転移のような特異な領域では、相を跨ぐようなサンプル点を予め用意する必要がある。 順位交差のように、パラメータ領域によって基底状態と励起状態がクロスするような場合にも、 サンプル波動関数のなかに、基底状態と励起状態の両方が含まれるようにすることで、精度良く計算できる。

8.2.1. Eigenvector continuation法を用いた近似殻模型波動関数の構築

配置間相互作用法においてEC法の有用性をいち早く検証したのは、S.König et al., Phys. Lett. B 810, 10, 135814 (2020)で、Full CI法を用いて得られた\({}^4\mathrm{He}\)の基底状態波動関数について、カイラル核力のlow-energy constants (LECs)に対する不定性評価(感度分析)をやってのけた。 これは、EC法なしではとても実現できない計算である。 上記の仕事では、NNLOまでの16個のLECのうち3個のLECに対する不定性の評価を行っている。

その後、筆者らは、より多くのパラメータを含む系(現象論的な相互作用を用いた殻模型計算)でEC法の有用性を検証した→S. Yoshida and Noritaka Shimizu, PTEP 2022 053D02

現象論的な相互作用は、アイソスピン対称性を陽に仮定しても\(sd\)殻で66個、\(pf\)殻で199の1体・2体の行列要素を持つ。 このような多次元のパラメータ空間においても、25-50点程度のサンプル点で、数%以下の誤差で波動関数を再現できることを示した。 また、近似波動関数を構成できれば、それをLanczos法の初期ベクトルとして使うことで、収束性を向上させる前処理的な用途にも使えることを示している。

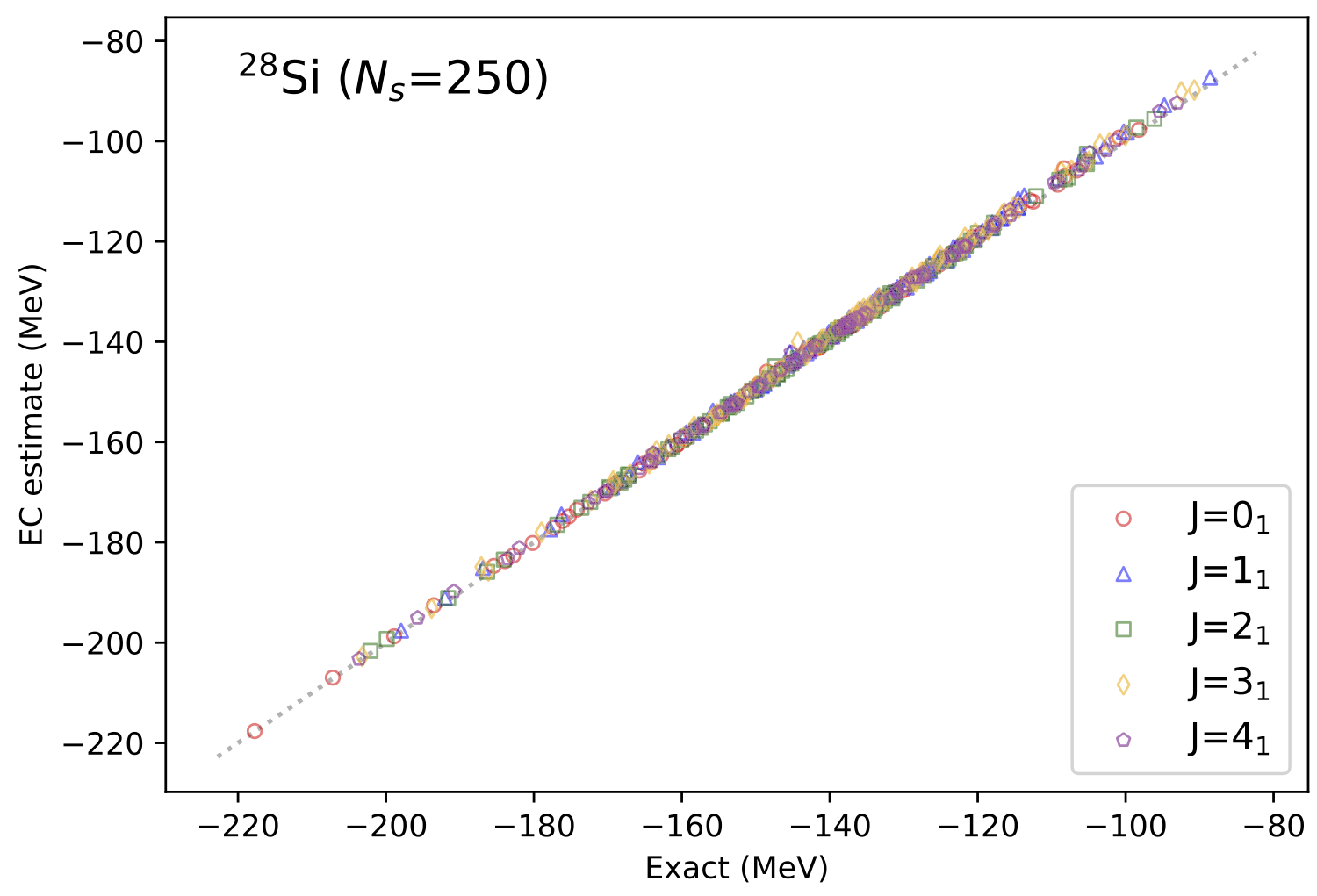
上に、sd殻の殻模型におけるEC法による予測結果を示した。横軸が厳密解、縦軸がEC法による予測値で、ほとんど対角線上に乗っていることがわかる。 ここで対象としている核は\({}^{28}\mathrm{Si}\)で、この核はsd殻において最も大次元\(\approx 90,000\)次元の行列の対角化に対応する。 角運動量の異なる\(J=0,1,2,3,4\)の5つの状態について、50点ほどで波動関数をサンプルしてやれば、 図のように(正規分布やラテン超方格で生成した)ランダムパラメータ(100)点における波動関数を、励起状態も含めて、平均して1%以下の誤差で予測できることが示された。

CI計算は、解くべき問題は一般に大変なものの、Lanczos法の性質上、基底状態とともに励起状態の波動関数も特段の違いなく得ることができるため、 一度サンプル波動関数を構築してしまえば、様々な状態・物理量(電磁遷移行列要素など)を系統的に調べることができる。

有名な殻模型相互作用の波動関数のデータベースを用意しておいて、そこからユーザーは必要な波動関数を取り出して近似波動関数を用いる、 といった方法論も将来的にありえるかもしれない。

8.3. pairing Hamiltonianでのデモ

以下では、pairing Hamiltonianを用いて、Eigenvector Continuation法によるFull-CIの波動関数を用いたパラメータ空間での内挿・外挿をしてみよう。

パラメータ空間(今はpairing strengthで1次元)において、サンプル点をいくつか取り、それを用いて別のパラメータ点での波動関数を予測する。 ターゲットとなるHamiltonianを\(H(g_{\odot})\)とすると、評価すべき行列要素は

\[\begin{split} \begin{align} H_{ij} & = \langle \psi(g_i) | H(g_{\odot}) | \psi(g_j) \rangle \nonumber \\ N_{ij} & = \langle \psi(g_i) | \psi(g_j) \rangle \nonumber \end{align} \end{split}\]

である。\(\ket{\psi(g_i)}\)は、\(g=g_i\)におけるFull-CI波動関数である。

殻模型ハミルトニアンの場合は、transition densityを計算することで\(H_{ij}\)の評価を大幅に効率化できる。 詳しくは、S. Yoshida and Noritaka Shimizu, PTEP 2022 053D02を参照。

実際のEC法の適用では、とくに\(H_{ij}\)の評価がコストが高いため、工夫が必要であるが、 pairing Hamiltonianの場合は、\(H_{ij}\ket{\psi(g)}\)を陽に計算して行列要素を評価することにする。

これまでの章でみてきたように、pairing Hamiltonianのもとでの基底状態は\(g_\mathrm{crit}\)を境にその性質が変わる。 したがって、サンプルする点の取り方に対して精度がどのように変わるかもあわせてみることにしよう。

そこで、サンプル点を以下のように取ったパターンを考える:

• Set-A: \(\{ -1.0, -0.50, 0.0 \}\)

• Set-B: \(\{ -1.0, 0.0, 1.0 \}\)

• Set-C: \(\{ 0.0, 0.50, 1.0 \}\)

また、予測点は\(g \in [-2.0, 2.0]\)の範囲で、\(0.1\)刻みで取ることにする。

\(N_\mathrm{orb}=8, N_\mathrm{occ}=4\)の場合について、上記のサンプル点を用いて、予測点における波動関数を予測してみよう。 なお、縮退を仮定して解く場合のFull-CIではこの場合次元が6と大変小さいため、サンプル数が多いとby definitionで厳密解が得られることに注意しよう。

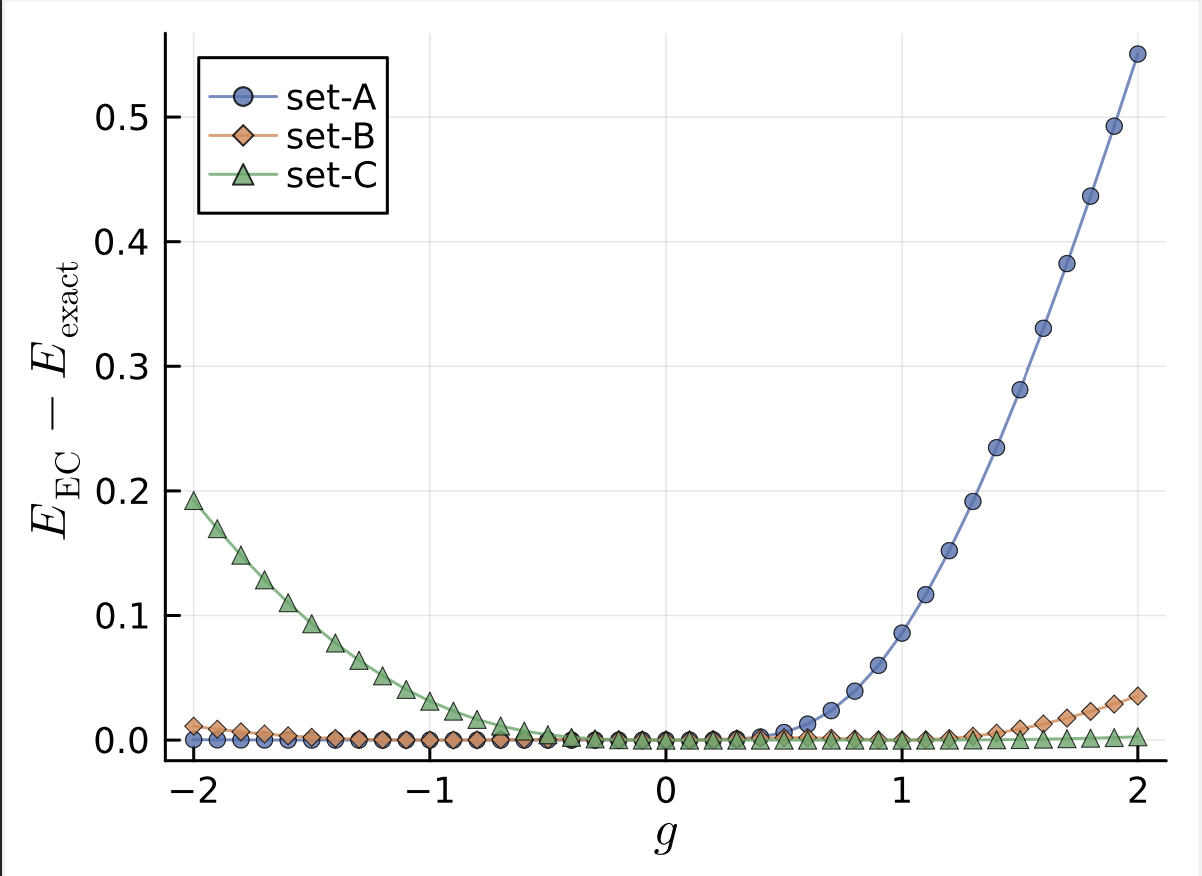
それぞれ、重点的にサンプルした領域においては、EC法による予測が非常に精度良く行われていることがわかる。 一方で、両方にまたがってサンプル点を取ったSet-Bの場合はどちらの相(というと不正確だが)においても、比較的よく内挿・外挿が出来ている.