In-medium Similarity Renormalization Group (IM-SRG)

7. In-medium Similarity Renormalization Group (IM-SRG)#

この章では、In-medium Similarity Renormalization Group(IM-SRG)法の概要と実装について説明する。

IMSRG法は原子核の基底状態の第一原理計算手法(post-HF法の意味で)としてだけでなく、殻模型の有効相互作用(バレンス空間の有効核力)・有効演算子の導出にも用いられるなど、応用上も非常に重要な手法である。

原子核分野では、HamiltonianのSoft化という文脈でSimilarity Renormalization Group(SRG)法が適用された後、その拡張としてIMSRG法が提案された。

SRGの基本的な考え方は、Hamiltonianのユニタリ変換である。元のHamiltonianを\(H_0\)、新しいHamiltonianを\(H_s\)とすると、

\[ H_s = U(s) H_0 U^\dagger(s) \]

と変換していくことで、２体系・３体系の物理量を変えずに多体計算の収束性を改善するソフトなHamiltonianを得ることができる。ただし実用上はトリックがあり、induceされる多体力をすべて取り扱うことはできず、ユニタリ性は厳密には保たれない。

7.1. IM-SRG flow equation#

\[\begin{split} \begin{align} \frac{dE}{ds} &= \sum_{ab} (n_a-n_b) \eta^{(1)}_{ab} f_{ba} + \frac{1}{2} \sum_{abcd} \eta^{(2)}_{abcd} \Gamma_{cdab} n_an_b \bar{n}_c \bar{n}_d \nonumber \\ \frac{df_{pq}}{ds} &= \sum_{a} (1+P_{pq}) \eta^{(1)}_{pa} f_{aq} + \sum_{ab} (n_a-n_b) (\eta^{(1)}_{ab} \Gamma_{bpaq} - f_{ab} \eta^{(2)}_{bpaq}) \nonumber \\ & + \frac{1}{2} \sum_{abc} (n_an_b\bar{n}_c + \bar{n}_a \bar{n}_b n_c) (1+P_{pq}) \eta^{(2)}_{cpab} \Gamma_{abcq} \nonumber \\ \frac{d\Gamma_{pqrs}}{ds} &= \sum_{a} \left\{ (1-P_{pq}) (\eta^{(1)}_{pa} \Gamma_{aqrs} - f_{pa} \eta^{(2)}_{aqrs}) -(1-P_{rs}) (\eta^{(1)}_{ar} \Gamma_{pqas} - f_{ar} \eta^{(2)}_{pqas}) \right\} \nonumber \\ & + \frac{1}{2} \sum_{ab} (1-n_a-n_b) (\eta^{(2)}_{pqab} \Gamma_{abrs} - \Gamma_{pqab} \eta^{(2)}_{abrs})\nonumber \\ & - \sum_{ab} (n_a - n_b) (1-P_{pq})(1-P_{rs}) \eta^{(2)}_{bqas} \Gamma_{apbr} \nonumber \end{align} \end{split}\]

7.2. Choice of Generator \(\eta\)#

IM-SRG flowのgenerator \(\eta\) の選び方は、flow equationのstiffness、つまり解きやすさや数値的な安定性に大きく影響を及ぼす。

件のLecture Noteでは、Wegner, imaginary time, Whiteの３つの選択肢を挙げ、ODE solverを適切に選ぶことで同程度の精度が得られることも示されている。そこで、本資料では、下記のWhiteのgeneratorを用いることにした。

\[\begin{split} \begin{align} \eta & = \eta^{(1)} + \eta^{(2)} \\ & = \frac{1}{2} \sum_{ph} \arctan\left(\frac{f_{ph}(s)}{\Delta_{ph}(s)}\right) \{ a^\dagger_p a_h \} + \frac{1}{8} \sum_{pp'hh'} \arctan\left(\frac{2 \Gamma_{pp'h'h}(s)}{\Delta_{pp'hh'}(s)}\right) \{ a^\dagger_p a^\dagger_{p'} a_h a_{h'} \} - H.c.. \end{align} \end{split}\]

形状からもわかるように,\(\eta\)はparticle-hole間(1-body)とpp-hh間(2-body)にのみ値を持つ。 IMSRG-flowでは、このparticle-hole間の成分がくりこまれていく(\(s \to \infty\)で小さくなる)。

7.3. IMSRGの実装#

globalなpairing potentialであることを利用して、上の表式を簡略化できないであろうか？

そのためには、\(\Gamma_{pqrs}(s)\)が\(p,q,r,s\)の4つのインデックスに対してどう依存し、 flowでどのような変化が起こるかに注目してみよう。

使えそうなのは、\(\eta\)がanti-hermitian(対角成分は0, \(\eta^{(1)}_{ij} = -\eta^{(1)}_{ji}\))であることと、以下の初期条件である。

\[\begin{split} \begin{align} f_{ij}(s=0) &= \delta_{ij} f_{ii} \\ \Gamma_{pqrs}(s=0) &= \delta_{q\bar{p}} \delta_{s\bar{r}} \Gamma_{p\bar{p}r\bar{r}} \end{align} \end{split}\]

これらを用いて、\(\Gamma_{pqrs}(s)\)のflow方程式を考えると:

\[\begin{split} \begin{align} \left. \frac{d\Gamma_{pqrs}}{ds} \right|_{s=0} &= \sum_{a} \left\{ \left( \eta^{(1)}_{pa} \Gamma_{aqrs} - f_{pa} \eta^{(2)}_{aqrs} \right) - \left( \eta^{(1)}_{qa} \Gamma_{aprs} - f_{qa} \eta^{(2)}_{aprs} \right) - \left( \eta^{(1)}_{ar} \Gamma_{pqas} - f_{ar} \eta^{(2)}_{pqas} \right) + \left( \eta^{(1)}_{as} \Gamma_{pqar} - f_{as} \eta^{(2)}_{pqar} \right) \right\} \nonumber\\ & + \frac{1}{2} \sum_{ab} (1-n_a-n_b) (\eta^{(2)}_{pqab} \Gamma_{abrs} - \Gamma_{pqab} \eta^{(2)}_{abrs})\nonumber \\ & - \sum_{ab} (n_a - n_b) (1-P_{pq})(1-P_{rs}) \eta^{(2)}_{bqas} \Gamma_{apbr} \nonumber \end{align} \end{split}\]

pairing Hamiltonianのような１粒子軌道が既に対角的\(f_{ij}\propto \delta_{ij}\)な場合、\(\eta^{(1)}\)は恒常的に0となる。

7.4. particle-hole channelの計算#

\(d\Gamma_{pqrs}/ds\)の計算を考える際の計算量は、最後の第3項が支配的である。

\[ \begin{align} \frac{d\Gamma_{pqrs}}{ds} & = ... - \sum_{ab} (n_a - n_b) (1-P_{pq})(1-P_{rs}) \eta^{(2)}_{bqas} \Gamma_{apbr} \end{align} \]

を見れば明らかなように、\(pqrs\)成分の更新に、\(ab\)のsummationが含まれるため、naiveには\(O(N^6)\)の計算量がかかる。一方で、第2項は、\(\eta^{(2)}_{pqab} \Gamma_{abrs}\)と、行列-行列積の形をしているため、 \((1-n_a-n_b)\)を表す対角行列(\(ab\)が\(pp\)か\(hh\)のときのみ有限の値を持つ)を用意しておけば、BLASを用いて効率よく計算できる。

以下では、第3項を効率よく計算する方法について考えてみよう。

7.5. 結果の解釈#

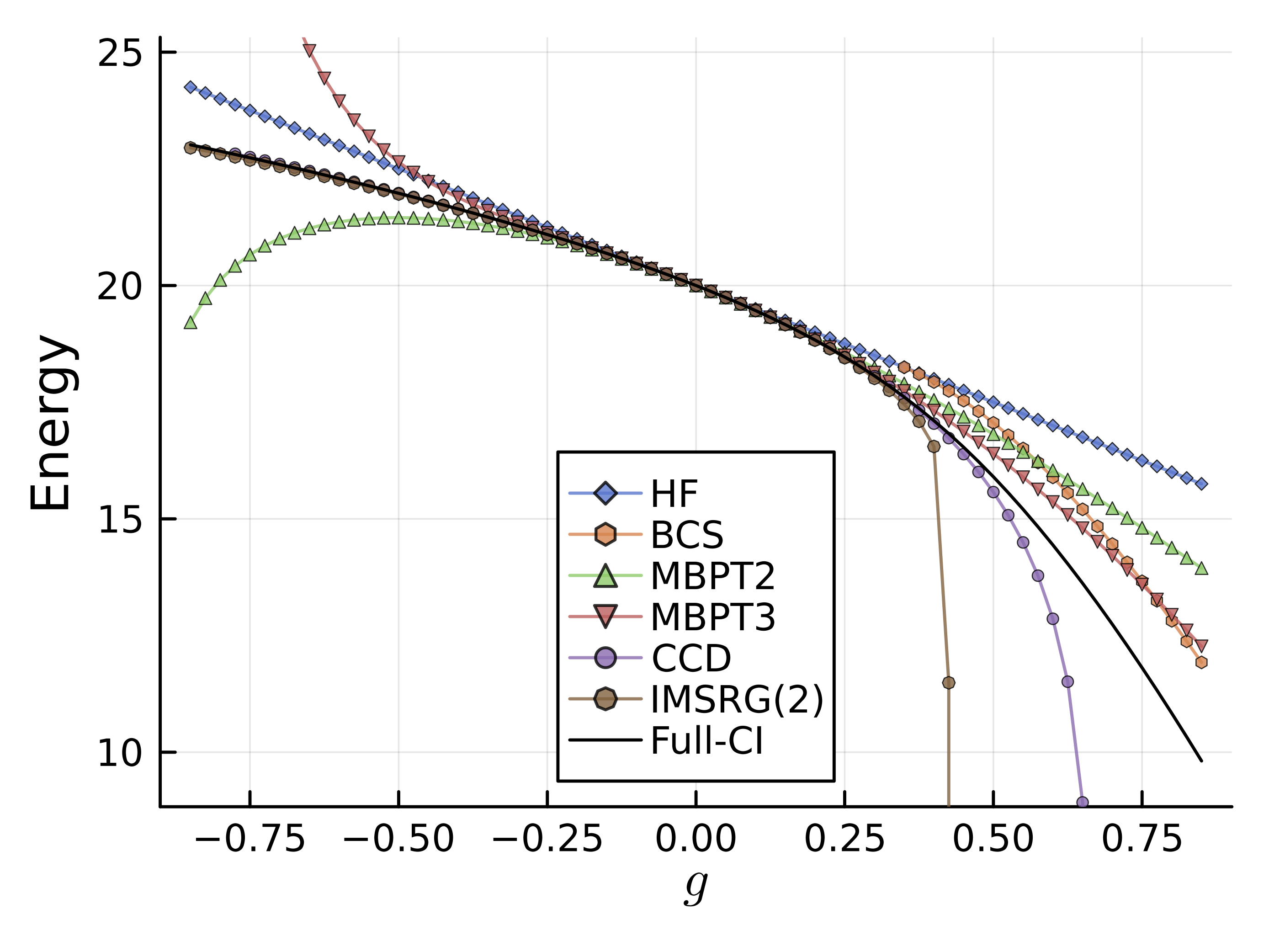
\(g\)が正で大きい領域では計算が収束せずに、エネルギーが発散してしまう。これは、IMSRGのflow equationが、\(g\)が大きい領域での計算には適していないことを示している。というのも、そもそもIMSRG-flowのgeneratorは、reference stateに対する励起をdecoupleすることを目的としていたわけだが、 Full-CIの章でみたように\(g >> 1\)の領域では、reference stateに対する様々な励起が同程度の重要性を持つため、decoupleがうまくいかないのである。

\(g\)が負の領域では、CCDよりもわずかに悪い結果となるが、この理由はcoupled clusterの章で書いたとおり、CCとIMSRGの各次数でどのダイアグラムが取り入れられるかの違いに由来する。