14. pytketを用いたVQE計算#
この章では、Quantinuumによるpytketを使ったVQE計算について述べる。 pytket user guideが役に立つ。
大きな注意点としては、(大変ややこしいことに)pytketの回転ゲートの角度パラメータは\(\pi/2\)単位で与えられることである。
#必要に応じて...
#!pip install pytket
#!pip install pytket-qiskit
#!pip install pytket-projectq
#!pip install openfermion
#!pip install seaborn
import numpy as np
import itertools
from itertools import combinations
import seaborn as sns
cols = sns.color_palette("deep")
import matplotlib.pyplot as plt
import pandas as pd
from openfermion import QubitOperator
from pytket.circuit import Circuit, Qubit, Bit
from pytket.circuit.display import render_circuit_jupyter as draw
from pytket.utils import gate_counts
from pytket.utils import probs_from_state
from pytket.utils.expectations import get_operator_expectation_value
from pytket.extensions.qiskit import AerStateBackend
from pytket.extensions.qiskit import AerBackend
Hamiltonianなどを再び書き写しておいて...
Show code cell source
class PairingHamiltonian:
def __init__(self, Norb, Nocc, gval, delta_eps=1.0):
self.Norb = Norb
self.Nocc = Nocc
self.delta_eps = delta_eps
self.gval = gval
self.basis = self.make_basis()
self.epsilon = self.eval_epsilon()
self.Hmat = self.eval_Hmat()
def make_basis(self):
self.basis = []
for occ in combinations(range(self.Norb), self.Nocc):
self.basis.append(occ)
return self.basis
def eval_epsilon(self):
self.epsilon = [ 2 * i * self.delta_eps for i in range(self.Norb) ]
return self.epsilon
def eval_Hmat(self):
dim = len(self.basis)
self.Hmat = np.zeros((dim, dim))
for bra_idx, bra in enumerate(self.basis):
for ket_idx, ket in enumerate(self.basis):
# Hamming distance
diff = [ i for i in bra if i not in ket ]
same = [ i for i in bra if i in ket ]
# for SPE term
if bra_idx == ket_idx:
self.Hmat[bra_idx, ket_idx] += np.sum( [self.epsilon[i] for i in same])
self.Hmat[bra_idx, ket_idx] += - self.gval * len(same)
# for pairing term
if len(diff) == 1:
self.Hmat[bra_idx, ket_idx] = - self.gval
return self.Hmat
def tuple_to_bitstring(tup, Norb, rev=True):
bitint = 0
for i in tup:
bitint += 2**i
if rev:
bitstring = "|"+format(bitint, f'0{Norb}b')[::-1]+">"
else:
bitstring = "|"+format(bitint, f'0{Norb}b')+">"
return bitstring
Norb = 4
Nocc = 2
gval = 0.33
Hamil = PairingHamiltonian(Norb, Nocc, gval)
evals, evecs = np.linalg.eigh(Hamil.Hmat)
evals = np.linalg.eigvalsh(Hamil.Hmat)
Egs_exact = evals[0]
E_HF = Hamil.Hmat[0,0]
print("basis:", Hamil.basis)
print([tuple_to_bitstring(tup, Norb) for tup in Hamil.basis])
print("eps: ", Hamil.epsilon)
print("Hmat: ", Hamil.Hmat)
print("evals: ", evals)
print("Egs_exact: ", Egs_exact, " E_HF", E_HF)
print("gs evec", evecs[:,0])
print("gs prob", evecs[:,0]**2)
params_exact = 0.5* np.array(
[-0.48104276, -1.03976498, -0.98963981, -1.18481738, -0.54832984]
)
# pytketの回転ゲートはpi/2単位で指定するので、pi/2で割っておく
params_exact = params_exact #
basis: [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
['|1100>', '|1010>', '|1001>', '|0110>', '|0101>', '|0011>']
eps: [0.0, 2.0, 4.0, 6.0]
Hmat: [[ 1.34 -0.33 -0.33 -0.33 -0.33 0. ]
[-0.33 3.34 -0.33 -0.33 0. -0.33]
[-0.33 -0.33 5.34 0. -0.33 -0.33]
[-0.33 -0.33 0. 5.34 -0.33 -0.33]
[-0.33 0. -0.33 -0.33 7.34 -0.33]
[ 0. -0.33 -0.33 -0.33 -0.33 9.34]]
evals: [1.18985184 3.29649666 5.34 5.34 7.42853393 9.44511758]
Egs_exact: 1.1898518351360725 E_HF 1.3399999999999999
gs evec [0.97121327 0.18194077 0.09817385 0.09817385 0.06360816 0.01789242]
gs prob [9.43255208e-01 3.31024447e-02 9.63810492e-03 9.63810492e-03
4.04599822e-03 3.20138762e-04]
14.1. pytketでの回路作成#
14.1.1. Givens rotation#
どうやらpytketにはGivens rotationの実装がなさそうなので自作しておく
def cG1(circ, c_qubit, i, j, theta):
theta_4 = theta / 4 / (np.pi/2)
circ.CX(i,j)
circ.Ry(theta_4, i)
circ.CX(j,i)
circ.Ry(-theta_4, i)
circ.CX(c_qubit, i)
circ.Ry(theta_4, i)
circ.CX(j,i)
circ.Ry(-theta_4, i)
circ.CX(c_qubit, i)
circ.CX(i,j)
def G(circ, i, j, theta):
theta_2 = theta / 2 / (np.pi/2)
circ.CX(i,j)
circ.Ry(theta_2, i)
circ.CX(j,i)
circ.Ry(-theta_2, i)
circ.CX(j,i)
circ.CX(i,j)
\(\pi/4\)回転が正しいかチェック。角度が\(\pi/2\)単位である仕様に注意しつつ...
circ_G = Circuit(2)
circ_G.X(0)
G(circ_G, 0, 1, np.pi/4 / (np.pi/2))
draw(circ_G)
backend = AerStateBackend()
transpiled = backend.get_compiled_circuit(circ_G, optimisation_level=2)
job = backend.process_circuit(transpiled)
result = backend.get_result(job)
statevector_ftqc = result.get_state()
# 1e-10 未満の確率は表示しない
probs_from_state(statevector_ftqc, min_p=1e-10)
{(0, 1): 0.22984884706592998, (1, 0): 0.7701511529340701}
できた。
14.1.2. Full-CI ansatz#
では次に、軌道が4つ、占有数が2に対応する回路を考え、\(g=0.33\)の結果を再現する角度パラメータを指定してやると...
# Ansatz for Norb=4, Nocc=2
my_circ_1 = Circuit(Norb)
# HF
my_circ_1.X(0)
my_circ_1.X(1)
# HF + pair excitations expressed by G and cG1
G(my_circ_1, 1, 2, params_exact[0])
G(my_circ_1, 2, 3, params_exact[1])
cG1(my_circ_1, 2, 0, 1, params_exact[2])
cG1(my_circ_1, 3, 0, 1, params_exact[3])
cG1(my_circ_1, 3, 1, 2, params_exact[4])
draw(my_circ_1)
gate_counts(my_circ_1)
Counter({<OpType.CX: 45>: 26, <OpType.Ry: 35>: 16, <OpType.X: 23>: 2})
回路を保存することもできる:
import pickle
with open("circuit_pytket.pkl","wb") as f:
pickle.dump(my_circ_1,f)
では、状態作成したものを測定し確率を計算してみよう。statevectorを使うことにする。
circ = my_circ_1.copy()
# initialize backend with default settings
backend = AerStateBackend()
# transpile and optimize for backend at level = 2
# optimisation... British spelling なぜならQuantinuumはCambridge Quantumから来ているから。
circ_compiled = backend.get_compiled_circuit(circ, optimisation_level=2)
gate_counts(circ_compiled)
job = backend.process_circuit(circ_compiled)
result = backend.get_result(job)
statevector = result.get_state()
statevector[ np.abs(statevector) > 1e-10 ]
array([0.01788929-8.66020112e-17j, 0.06360699-2.88837067e-16j,
0.09817351-4.82563346e-16j, 0.09817219-3.94005123e-16j,
0.18193913-7.09880803e-16j, 0.97121391-5.57798065e-15j])
probs_from_state(statevector, min_p=1e-10) # 1e-10 未満の確率は表示しない
{(0, 0, 1, 1): 0.00032002678223212646,
(0, 1, 0, 1): 0.004045849260479198,
(0, 1, 1, 0): 0.009638037703111972,
(1, 0, 0, 1): 0.00963777971356642,
(1, 0, 1, 0): 0.03310184865198989,
(1, 1, 0, 0): 0.9432564578886204}
厳密解における各状態の確率を再現できた。
14.2. pytketでの演算子表現#
pytketでもHamiltonianの表現方法は幾つかある。ひとつはOpenFermionのQubitOperatorを用いる方法で...
# Qubit Hamiltonian
SPEs = Hamil.epsilon
obs = [ ]
coeffs = [ ]
H_qubit = QubitOperator()
## 1-Zp term
for i in range(Hamil.Norb):
H_qubit += ( 0.5 * (SPEs[i] - Hamil.gval) * (QubitOperator('') - QubitOperator('Z'+str(i)) ) )
## XX+YY term proportional to g (pairing strength)
for i in range(Hamil.Norb):
for j in range(i+1, Hamil.Norb):
if i == j:
continue
factor = - Hamil.gval / 2
XX = QubitOperator('X'+str(i)+' X'+str(j), factor)
YY = QubitOperator('Y'+str(i)+' Y'+str(j), factor)
H_qubit += XX
H_qubit += YY
print("H_qubit: ", H_qubit)
H_qubit: 5.34 [] +
-0.165 [X0 X1] +
-0.165 [X0 X2] +
-0.165 [X0 X3] +
-0.165 [Y0 Y1] +
-0.165 [Y0 Y2] +
-0.165 [Y0 Y3] +
0.165 [Z0] +
-0.165 [X1 X2] +
-0.165 [X1 X3] +
-0.165 [Y1 Y2] +
-0.165 [Y1 Y3] +
-0.835 [Z1] +
-0.165 [X2 X3] +
-0.165 [Y2 Y3] +
-1.835 [Z2] +
-2.835 [Z3]
DocumentのExpectation valuesを参考にしつつ、pytketのQubitPauliOperatorに変換してみよう。
from pytket.pauli import Pauli, QubitPauliString
from pytket.utils.operators import QubitPauliOperator
pauli_sym = {"I": Pauli.I, "X": Pauli.X, "Y": Pauli.Y, "Z": Pauli.Z}
def qps_from_openfermion(paulis):
"""Convert OpenFermion tensor of Paulis to pytket QubitPauliString."""
qlist = []
plist = []
for q, p in paulis:
qlist.append(Qubit(q))
plist.append(pauli_sym[p])
return QubitPauliString(qlist, plist)
def qpo_from_openfermion(openf_op):
"""Convert OpenFermion QubitOperator to pytket QubitPauliOperator."""
tk_op = dict()
for term, coeff in openf_op.terms.items():
string = qps_from_openfermion(term)
tk_op[string] = coeff
return QubitPauliOperator(tk_op)
hamiltonian_op = qpo_from_openfermion(H_qubit)
hamiltonian_op
{(): 5.34000000000000, (Zq[0]): 0.165000000000000, (Zq[1]): -0.835000000000000, (Zq[2]): -1.83500000000000, (Zq[3]): -2.83500000000000, (Xq[0], Xq[1]): -0.165000000000000, (Yq[0], Yq[1]): -0.165000000000000, (Xq[0], Xq[2]): -0.165000000000000, (Yq[0], Yq[2]): -0.165000000000000, (Xq[0], Xq[3]): -0.165000000000000, (Yq[0], Yq[3]): -0.165000000000000, (Xq[1], Xq[2]): -0.165000000000000, (Yq[1], Yq[2]): -0.165000000000000, (Xq[1], Xq[3]): -0.165000000000000, (Yq[1], Yq[3]): -0.165000000000000, (Xq[2], Xq[3]): -0.165000000000000, (Yq[2], Yq[3]): -0.165000000000000}
あるいはQiskitのSparsePauliOpを変換しても良い。
pytketのdocumentに、コード例が書いてあるが、(2025年4月時点では)Qiskitのbitの並び方を意識しない書き方になっていて誤りがあるので、注意が必要だ。
from qiskit.quantum_info import SparsePauliOp
from pytket.pauli import Pauli, QubitPauliString
from pytket.utils.operators import QubitPauliOperator
from pytket import Qubit
from collections import defaultdict
def qps_from_sparsepauliop(paulis):
"""Convert SparsePauliOp tensor of Paulis to pytket QubitPauliString."""
pauli_sym = {"I": Pauli.I, "X": Pauli.X, "Y": Pauli.Y, "Z": Pauli.Z}
qlist = []
plist = []
for q, p in enumerate(paulis):
if p != "I":
qlist.append(Qubit(q))
plist.append(pauli_sym[p])
return QubitPauliString(qlist, plist)
def qpo_from_sparsepauliop(sp_op):
"""
Convert SparsePauliOp QubitOperator to pytket QubitPauliOperator.
"""
tk_op = defaultdict(complex)
for term, coeff in sp_op.to_list():
# ↓の追加が必要
term = term[::-1]
string = qps_from_sparsepauliop(term)
tk_op[string] += coeff
return QubitPauliOperator(tk_op)
op_qiskit = SparsePauliOp.from_list( list(zip(["IIIZIZ"], [-0.5] )))
qpo_from_sparsepauliop(op_qiskit)
{(Zq[0], Zq[2]): -0.500000000000000}
14.2.1. エネルギーの測定#
作ったansatzとHamiltonian operatorを、指定したバックエンドに投げて
pytket.utils.expectationsに用意されたget_operator_expectation_value関数で期待値を測定してみよう。
回路とオブザーバブル(に対応する演算子)を指定する、QiskitでいうとEstimatorのようなものだ。
以下ではQiskit AerのStatevecvtor simulatorを用いる。
ansatz = my_circ_1.copy()
backend = AerStateBackend()
E_ftqc = get_operator_expectation_value(ansatz, hamiltonian_op, backend=backend)
print("E_ftqc: ", E_ftqc, "Egs_exact: ", Egs_exact, "E_HF: ", E_HF)
E_ftqc: 1.1898518352304368 Egs_exact: 1.1898518351360725 E_HF: 1.3399999999999999
Z基底での測定結果を集めるQiskitでいうSampler的な使い方をしたい場合は、backendを指定して回路とショット数などを指定すると良い。
from pytket.extensions.qiskit import AerBackend
ansatz = my_circ_1.copy()
ansatz.measure_all()
pytket_backend = AerBackend()
results = pytket_backend.run_circuit(ansatz, n_shots=4096)
results.get_counts()
Counter({(1, 1, 0, 0): 3853,
(1, 0, 1, 0): 140,
(1, 0, 0, 1): 45,
(0, 1, 1, 0): 43,
(0, 1, 0, 1): 13,
(0, 0, 1, 1): 2})
14.3. 回路パラメータの最適化#
pytketを使ったVQE計算(回路の最適化)も試してみよう。
(pytketで勾配降下やAdamなどの最適化手法を使った方法がすぐにはわからなかったので)Nakanishi-Fujii-Todo法を実装して、逐次最適化してみよう。 参考: Phys. Rev. Research 2, 043158 (2020)
ざっと要点だけ説明すると、Nakanishi-Fujii-Todo法は、gradient freeなsequential optimizationの方法の一つ。
N個のパラメータに依存する1個の量子ゲートのパラメータに着目し、その値を最適化したいとき、 パラメータの周期を取り尽くす等間隔な2N+1点でエネルギーを測ると、エネルギーは周期関数になる。 その結果を離散フーリエ変換して、最小のエネルギーを求める点を推定し、これを各ゲートに対して収束するまで繰り返していく。
いま上の例で最適化したい回路はGivens rotationやcontrolled Givens rotationである。
上の自作関数を見てもわかるように、それぞれパラメータが符号も含めてそれぞれ2(4)個ある。
したがって、G(cG)の角度パラメータの最適化には5(9)点での計測が必要になる。
また、GやcGという量子ゲートを構成するすべての回転ゲートが周期を取り尽くすように測る必要があるため、
G(cG)の場合は関数の外から与える角度としては、\(4\pi(8\pi)\)周期分をカバーして測る必要がある。
Show code cell source
from scipy.optimize import minimize_scalar
def ansatz(params):
circ = Circuit(4)
circ.X(0)
circ.X(1)
G(circ, 1, 2, params[0])
G(circ, 2, 3, params[1])
cG1(circ, 2, 0, 1, params[2])
cG1(circ, 3, 0, 1, params[3])
cG1(circ, 3, 1, 2, params[4])
return circ
def objective(params):
circ = ansatz(params)
return (
get_operator_expectation_value(circ, hamiltonian_op, backend)
)
def draw_DFT_curve(xplot, DFTcurve, spot, Es, x_min, y_min):
fig = plt.figure(figsize=(3,3))
ax = fig.add_subplot(1,1,1)
ax.plot(xplot, DFTcurve, label="DFT curve", color=cols[0])
ax.scatter(spot, Es, marker="o", label="Measured", color=cols[1])
ax.scatter(x_min, y_min, marker="*", color=cols[3], label="Candidate")
ax.legend()
plt.show()
plt.close()
def eval_DFT_coeff(Es, spot):
N = len(Es)
DFT_coef = np.zeros(N, dtype=float)
for idx_M in range(N):
t_data = Es[idx_M]
for idx_coeff in range(N):
#print("idx_M", idx_M, "idx_coeff", idx_coeff)
if idx_coeff == N-1:
DFT_coef[idx_coeff] += t_data
#print("sum of Es??", DFT_coef[idx_coeff], "idx_M", idx_M, "t_data", t_data)
continue
theta_order = idx_coeff // 2 + 1
if idx_coeff % 2 == 0:
DFT_coef[idx_coeff] += 2 * t_data * np.cos(theta_order * spot[idx_M])
else:
DFT_coef[idx_coeff] += 2 * t_data * np.sin(theta_order * spot[idx_M])
DFT_coef /= N
if abs(np.mean(Es) - DFT_coef[-1]) > 1e-10:
print("Something wrong in DFT")
exit()
return DFT_coef
def func_DFT_coeff(DFT_coef):
def DFTcurve(x):
y = 0
for n in range(len(DFT_coef)):
if n == len(DFT_coef) - 1:
y += DFT_coef[n]
break
theta_order = n // 2 + 1
if n % 2 == 0:
y += DFT_coef[n] * np.cos( theta_order * x)
else:
y += DFT_coef[n] * np.sin( theta_order * x)
return y
return DFTcurve
def DFT(it, Es, spot, verbose, method="scipy"):
N_duration = (len(Es) - 1) // 2
DFT_coef = eval_DFT_coeff(Es, spot)
theta_current = spot[0]
xplot = np.linspace(theta_current, theta_current + N_duration * 2*np.pi, 100)
DFTcurve = func_DFT_coeff(DFT_coef)(xplot)
if method == "scipy":
obj = minimize_scalar(func_DFT_coeff(DFT_coef), bounds=(theta_current, theta_current + 2 * np.pi * N_duration))
x_min = obj.x
y_min = obj.fun
elif method == "naive":
idx_min = np.argmin(DFTcurve)
x_min = xplot[idx_min]
y_min = DFTcurve[idx_min]
if verbose and it % 10 == 0:
draw_DFT_curve(xplot, DFTcurve, spot, Es, x_min, y_min)
new_theta = x_min % (2 * np.pi * N_duration)
return new_theta
def NFTmethod(it, Ecurrent, params, which_Gate, verbose):
params_ = params.copy()
# Making point to measure for Discrete Fourier Transformation
# GやcG1で使われる角度は中で2(4)で割って使われる。これらが0から2piの範囲をカバーしなければならないことに注意してfactorをかけている。
if where_is_G_or_cG1[which_Gate] == "G":
spot = [params_[which_Gate]] + [ params_[which_Gate] + n * 2 * (2 * np.pi)/5 for n in range(1,5) ]
spot = np.array(spot)
elif where_is_G_or_cG1[which_Gate] == "cG1":
spot = [params_[which_Gate]] + [ params_[which_Gate] + n * 4 * (2 * np.pi)/9 for n in range(1,9) ]
spot = np.array(spot)
else:
print("Something wrong")
if verbose:
spot_in_2pi = spot.copy()
spot_in_2pi -= spot[0]
spot_in_2pi = spot_in_2pi / (2 * np.pi)
print("which_Gate", which_Gate, "type", where_is_G_or_cG1[which_Gate])
# Measure the energy at the spot
tmp = params_.copy()
Es = np.zeros(len(spot))
Es[0] = Ecurrent
for idx in range(1, len(spot)): # 0 is already measured
tmp[which_Gate] = spot[idx]
E = objective(tmp)
Es[idx] = E
if verbose:
print("Emeasured", Es)
param_best = DFT(it, Es, spot, verbose)
# Find a minimum point
params_[which_Gate] = param_best
return params_
np.random.seed(0)
where_is_G_or_cG1 = {0: "G", 1: "G", 2: "cG1", 3: "cG1", 4: "cG1"}
params = np.random.rand(5) * np.pi * 2
print("initial params", params)
E_initial = E_current = objective(params)
it_max = 100
verbose = True
stag = 0
print("Optimizing parameters...")
for it in range(it_max):
print("iteration %5d " % it, end="")
if it > 0:
verbose = False
E_prev = E_current
for which_Gate in np.random.choice(5, 5, replace=False):
params_ = NFTmethod(it, E_current, params, which_Gate, verbose)
E_new = objective(params_)
params = params_.copy()
E_current = E_new
print("Energy_opt %15.10f" % E_current)
if abs(E_current - E_prev) < 1e-8:
stag += 1
if stag > 3:
break
print("******************")
print("E_initial", E_initial, " 最適化 =>", E_current, "Egs_exact", Egs_exact, "diff.", E_current - Egs_exact)
print("******************")
initial params [3.44829694 4.49366732 3.78727399 3.42360201 2.66190161]
Optimizing parameters...
iteration 0 which_Gate 1 type G
Emeasured [1.4867657 1.79578918 1.63703289 1.47242273 1.89645555]
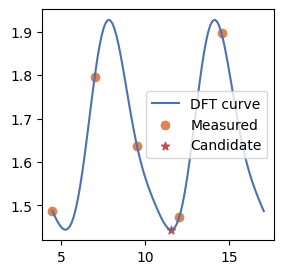
which_Gate 3 type cG1
Emeasured [1.44368379 1.83839806 1.5908143 1.79839549 1.8343694 1.6956903
1.95097955 1.52029136 1.90655423]
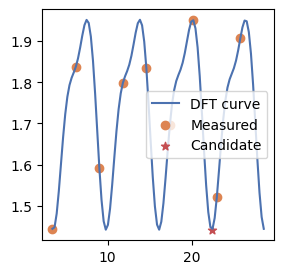
which_Gate 4 type cG1
Emeasured [1.44136355 1.57353789 1.47975579 1.54559194 1.53066566 1.49414067
1.56461717 1.4473691 1.57767619]
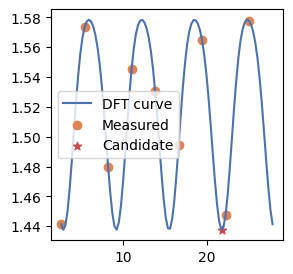
which_Gate 0 type G
Emeasured [1.43759698 1.93377273 4.07509191 4.9023242 3.27226269]
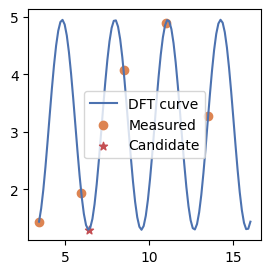
which_Gate 2 type cG1
Emeasured [1.29668783 1.33180213 1.25911905 1.35624767 1.24748919 1.36080235
1.26475917 1.33840335 1.29777327]
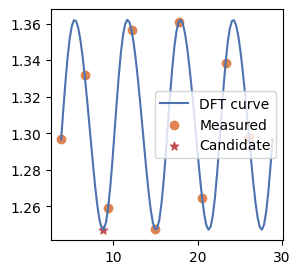
Energy_opt 1.2472132040
iteration 1 Energy_opt 1.1951439683
iteration 2 Energy_opt 1.1900667982
iteration 3 Energy_opt 1.1898545248
iteration 4 Energy_opt 1.1898518786
iteration 5 Energy_opt 1.1898518360
iteration 6 Energy_opt 1.1898518352
iteration 7 Energy_opt 1.1898518351
iteration 8 Energy_opt 1.1898518351
iteration 9 Energy_opt 1.1898518351
******************
E_initial 1.4867657043426625 最適化 => 1.1898518351361973 Egs_exact 1.1898518351360725 diff. 1.247890679678676e-13
******************
上の場合は、 statevectorを用いたので数回~10回程度で最適化が終了する、 実際には、simulatorの場合でもshotで測る場合はshot error、実機の場合は様々なノイズの影響を受けるが、 いずれにしても、回路の測定が高速にできればとても強力な最適化手法の一つである。
