Quantum Computing

9. Quantum Computing#

筆者には量子計算のgeneralな説明をするような能力は無いので、必要な最低限の情報をまとめておく。

より詳細が知りたい場合は、様々なTutorialや教材があるので、そちらを参照してほしい。

9.1. 基本的な量子ゲート#

9.1.1. 1-qubit ゲート#

1-qubitゲートは、1つの量子ビットに作用するゲートである。

\(\ket{0}\)と\(\ket{1}\)を基底とする1-qubitの状態ベクトルを\(\ket{ \psi } = \alpha \ket{0} + \beta \ket{1}\)とする。

qubitに対する演算はノルムを保存するユニタリ行列で表される。最も重要なものがパウリ行列である。

\[\begin{split} X = \left[ \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right], \quad Y = \left[ \begin{array}{cc} 0 & -i \\ i & 0 \end{array} \right], \quad Z = \left[ \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right], \quad \end{split}\]

また、下記に示すようなHadamardゲート(\(H\)), 位相ゲート(\(S\)), \(\pi/8\)ゲート(\(T\))もよく使われる。

\[\begin{split} H = \frac{1}{\sqrt{2}} \left[ \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right], \quad S = \left[ \begin{array}{cc} 1 & 0 \\ 0 & i \end{array} \right], \quad T = \left[ \begin{array}{cc} 1 & 0 \\ 0 & \exp(i \pi /4) \end{array} \right] \end{split}\]

\(H = (X+Z)/\sqrt{2}, \quad S = T^2\)といった関係が成り立つ。

Pauli行列を指数関数の肩に乗せたもの(各軸周りの回転)もよく使われる。

\[\begin{split} \begin{align} R_x(\theta) & = \exp(-i \theta X/2) = \left[ \begin{array}{cc} \cos(\theta/2) & -i \sin(\theta/2) \\ -i \sin(\theta/2) & \cos(\theta/2) \end{array} \right] \\ R_y(\theta) &= \exp(-i \theta Y/2) = \left[ \begin{array}{cc} \cos(\theta/2) & -\sin(\theta/2) \\ \sin(\theta/2) & \cos(\theta/2) \end{array} \right] \\ R_z(\theta) &= \exp(-i \theta Z/2) = \left[ \begin{array}{cc} \exp(-i \theta/2) & 0 \\ 0 & \exp(i \theta/2) \end{array} \right] \end{align} \end{split}\]

この回転ゲートを用いた重要な定理を示す。

定理

単一qubitに対する任意のユニタリ変換があるとき、\(U= \exp(i \alpha) R_z(\beta) R_y(\gamma) R_z(\delta)\)を満たす\(\alpha, \beta, \gamma, \delta\)が存在する。

9.1.2. 2-qubit ゲート#

2-qubitゲートは、2つの量子ビットに作用するゲートである。

2-qubitゲートの中で最も重要なものはCNOT(CX)ゲートで、制御ビットが0のときは何もしないが、制御ビットが1のときはターゲットビットにXゲートを作用させる。 その他の制御ユニタリゲート, SWAPゲート, iSWAPゲートなどもよく使われるが、以下に紹介するようにuniversalゲートセットが決まれば、それらのゲートを組み合わせて2-qubitゲートを作ることができる。

9.1.3. Universal gate set#

量子計算において、任意の量子ゲートを作るためには、ある特定のゲートセットがあれば十分である。このようなゲートセットをuniversal gate setと呼ぶ。 以下によく使われるuniversal gate setを示す。

  • 回転ゲート\(R_x(\theta), R_y(\theta), R_z(\theta)\)と位相ゲート\(S\)、CNOTゲート

  • Cliffordゲートセット\(\{ H, S, CNOT\}\) と \(T\)ゲート

  • ToffoliゲートとHadamardゲート

9.2. 重ね合わせ状態#

\[ \ket{0} \xrightarrow{H} \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \]

\(\ket{0}\)で初期化された\(N\)個のqubitについて、Hadamard gateを適用してみよう。

\[ \ket{0}^{\otimes N} \xrightarrow{H^{\otimes N}} \left( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \right) \otimes \cdots \otimes \left( \frac{\ket{0} + \ket{1}}{\sqrt{2}} \right) = \frac{1}{\sqrt{2^N}}\sum_{x=0}^{2^N-1}\ket{x} \]

最後の等式では、整数値\(0\)から\(2^N-1\)がビット列と対応することを用いた。

9.3. 量子テレポーテーション#

ある量子ビットの状態を量子のもつれを用いて別の量子ビットに移すことを量子テレポーテーションという。

Alice と Bob がいるとする。Alice が持っている量子ビットの状態を Bob に送ることを考える。 Alice と Bob は、物理的には離れていて、両者は古典的な通信しかできない一方で、 Alice と Bob は、量子もつれを共有している(もつれのある量子ビットを１つずつ持っている)とする。

このとき、Alice が持っている量子ビットの状態を Bob に送ることができる。 量子テレポーテーションの手順は以下の通りである。

  1. Alice と Bob は、もつれの量子ビットを共有し分け合う(\(q_1, q_2\))
    \( |q_1 q_2 \rangle \equiv \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle)\)

  2. Alice が送りたい量子ビットを\(q_0\)とする。 \( |q_0 \rangle = \alpha |0\rangle + \beta |1 \rangle\)

  3. Alice は、\(q_0 \to q_1\) に CNOT ゲートを適用する。
    \( | \psi \rangle = (\alpha |0\rangle + \beta |1 \rangle) \frac{1}{\sqrt{2}} (|00\rangle + |11\rangle) = \frac{\alpha}{\sqrt{2}} (|000\rangle + |011\rangle) + \frac{\beta}{\sqrt{2}} (|110\rangle + |101\rangle) \)

  4. Alice は、\(q_0\) に Hadamard ゲートを適用する。
    \( | \psi \rangle = \frac{\alpha}{2} \left( |000\rangle + |011\rangle + |100\rangle + |111\rangle \right) + \frac{\beta}{2} \left( |010\rangle + |001\rangle - |110\rangle - |101\rangle \right) \)

  5. Alice は、\(q_0\) と \(q_1\) を測定し、測定結果を Bob に送る。

  6. Bob は、受け取った測定結果に応じて、\(q_2\) に X ゲート、Z ゲートを適用することで、\(q_2\) に \(q_0\) の状態を再現することができる。

Aliceの5.の測定結果

Bobの持つ量子ビット\(q_2\)の状態

\(q_0\)を再現するための操作

00

\(\alpha |0\rangle + \beta |1\rangle\)

なし

01

\(\alpha |1\rangle + \beta |0\rangle\)

X ゲート

10

\(\alpha |0\rangle - \beta |1\rangle\)

Z ゲート

11

\(\alpha |1\rangle - \beta |0\rangle\)

X ゲート, Z ゲート

9.4. 演算子の期待値計算#

ターゲット量子ビット上にencodeされた状態\(\ket{\psi}\)に対して、演算子\(O\)の期待値を計算するための一般論を示す。

第2量子化されたハミルトニアン\(\hat{H}\)を量子コンピュータ上でシミュレートするためには、\(\hat{H}\)を量子ビット上にエンコードし、その期待値を計算する必要がある。より具体的には、"IZIII", "IXXII", ...のようなパウリ演算子のテンソル積を考える必要がある。

Pairing Hamiltonianの場合は、たかだか\(Z\)が単一 or 2つのqubitに\(XX\)または\(YY\)が作用する演算子しか現れない。 そこで、必要な期待値(より正確にはZ基底(computational basis)での期待値)を計算するための関数を用意しておこう。

通常、qubitの測定は\(Z\)基底で行われるため、\(X,Y\)の期待値を計算するためには、少し工夫が必要である。 よくこのことを指して、"basis rotation"などと呼ぶこともあるが、文献によって同じことを別の名前で呼ぶことがあるので注意が必要である。 \(X,Y\)を計測する際にはそれぞれHadamardゲート(\(S^{\dagger}\), Hadamardゲート)を適用して\(Z\)の期待値を計測してやれば良い:

\[\begin{split} \begin{align} \langle \psi | X | \psi \rangle & = \langle \psi | H Z H | \psi \rangle \\ \langle \psi | Y | \psi \rangle & = \langle \psi | S X S^{\dagger} | \psi \rangle = \langle \psi | S H Z H S^{\dagger} | \psi \rangle \end{align} \end{split}\]
def expec_Zstring(res, idx_relevant, Qiskit_ordering=True, target_qubits=[], ancilla_qubit=None):
    exp_val = exp_val_p0 = exp_val_p1 = 0.0
    n_shot = sum(res.values())
    n_qubit = len(list(res.keys())[0])
    idx_ancilla = None
    for bitstr, count in res.items():
        if ancilla_qubit != None and target_qubits != []:
            bitstr_target = ''.join([bitstr[k] for k in range(n_qubit) if k != idx_ancilla])
        else:
            bitstr_target = bitstr
        tmp = 1.0
        for idx in idx_relevant:
            if Qiskit_ordering:
                idx = -1 - idx
            bit = int(bitstr_target[idx])            
            tmp *= (1 - 2 * bit)
        exp_val += tmp * count
        
        if ancilla_qubit != None:
            if int(bitstr[idx_ancilla]) == 0:
                exp_val_p0 += tmp * count
            else:
                exp_val_p1 += tmp * count
    exp_val /= n_shot; exp_val_p0 /= n_shot; exp_val_p1 /= n_shot
    return exp_val, exp_val_p0, exp_val_p1

※これらの関数が正しく実装されているかは後ほど、Quantum Krylovの章でチェックしている。 また、どのフレームワークを使うかやStatevetor/Shot測定の別によって幾つか追加が必要なので詳細はそちらを参照してほしい。

以下ではより簡単な例として、\(\ket{\psi} = a \ket{11} + b \ket{10} + c \ket{01} + d \ket{00}\)に対して、\(X_0 \otimes X_1\)の期待値を計算することを考えてみよう。

\((X_0 \otimes X_1) \ket{\psi} = d \ket{11} + c \ket{10} + b \ket{01} + a \ket{00}\)であるから、期待値は\(\langle \psi | X_0 \otimes X_1 | \psi \rangle = a^*d + b^*c + c^*b + d^*a\)である。

import numpy as np
#import matplotlib.pyplot as plt
from qiskit import QuantumCircuit
from qiskit.quantum_info import Statevector
from qiskit_aer.primitives import SamplerV2
sampler = SamplerV2()

# 状態作成 Ryを0,1番目の量子ビットに適用して適当に作る。
np.random.seed(0)
qc_state = QuantumCircuit(2)
qc_state.ry(np.random.randn(), 0)
qc_state.ry(np.random.randn(), 1)

# Statevectorの計算
state_vector = Statevector.from_instruction(qc_state)
display(state_vector.draw('latex'))
a, b, c, d = state_vector.data

# X0X1の期待値を計算する回路 (shot測定)
qc = qc_state.copy()
qc.h(0)
qc.h(1)
state_vector = Statevector.from_instruction(qc)
display(state_vector.draw('latex'))

qc.measure_all()
sampler = SamplerV2()
job = sampler.run([qc], shots=10**5)
result = job.result()
counts = result[0].data.meas.get_counts()
counts
print("From statevector, a^*d + c^*b + b^*c + d^*a  =", np.conj(a)*d + np.conj(c)*b + np.conj(b)*c + np.conj(d)*a)
print("<X0X1> =", expec_Zstring(counts, [0, 1])[0])
\[0.622908812 |00\rangle+0.7566270503 |01\rangle+0.1263208434 |10\rangle+0.1534378151 |11\rangle\]
\[0.8296472605 |00\rangle-0.080417605 |01\rangle+0.5498886019 |10\rangle-0.0533006333 |11\rangle\]
From statevector, a^*d + c^*b + b^*c + d^*a  = (0.3823110686155987+0j)
<X0X1> = 0.38196

9.5. 量子コンピュータを用いた量子多体系の計算#

代表的な量子系に対するアルゴリズムについて説明する。

適宜、回路図を描きながら説明する。回路図を描くときには上位ビット(ビット列の左側)が上に来るようできるだけ統一して描いたつもりだが、Qiskitではビット列の右側が上に来るように描かれるのでそれに引っ張られて誤りがあるかもしれない。

9.5.1. VQE (Variational Quantum Eigensolver)#

第二量子化され、有限の配位で(近似的に)表現されるような系では、 ビット列の各ビットを量子ビットに割り当てて、その状態\(\ket{0}, \ket{1}\)をそれぞれ非占有/占有状態とみなせば あとはその重みとあわせて、(試行)波動関数を表現することができる。 ３つの軌道があり、粒子数が1の系を例に取れば以下のようにかける:

\[ \begin{align} \ket{\psi} = c_{001} \ket{001} + c_{010} \ket{010} + c_{100} \ket{100} \end{align} \]

典型的には、回転ゲートなどを組み合わせて各配位を作成することから、 回転角などのパラメータを持った試行波動関数として\(\ket{\psi(\theta)}\)と書く。 状態作成の模式図を描くと以下のようになる。

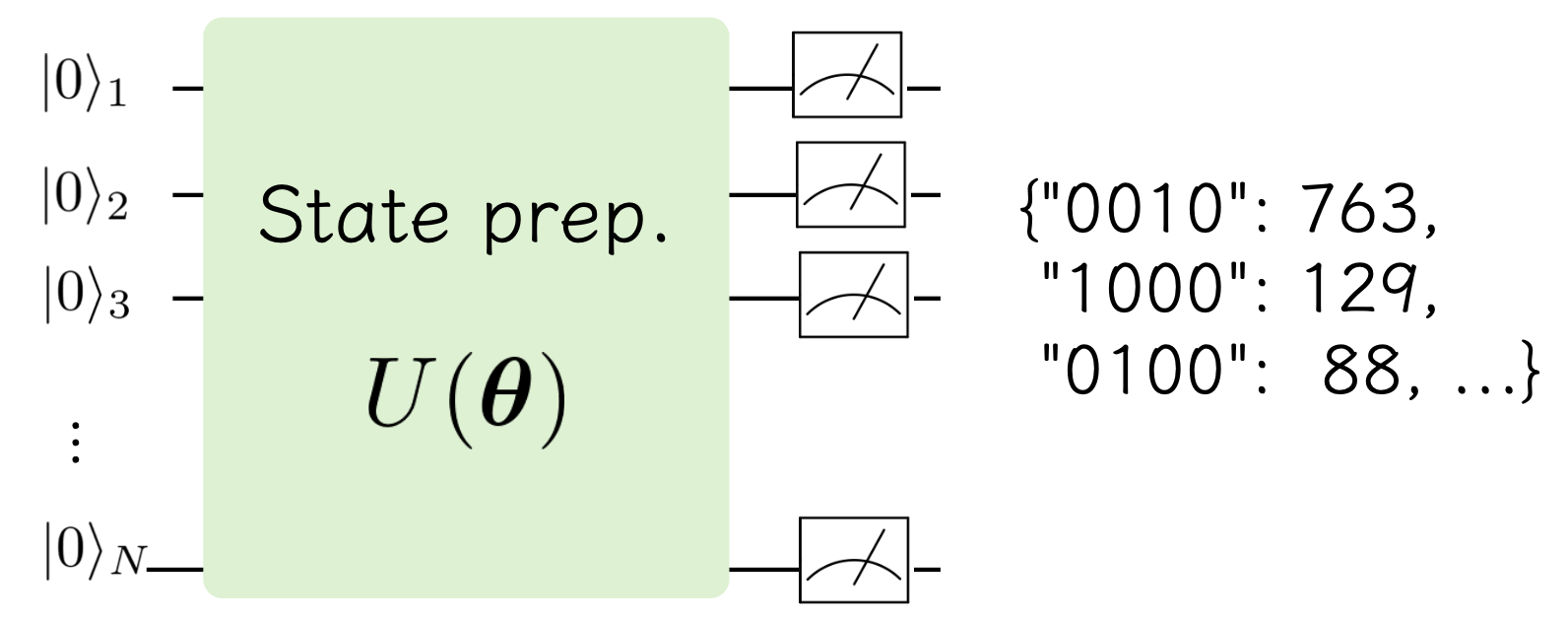
ユニタリ演算の組み合わせで表現される\(\ket{\psi(\theta)}\)を作成する回路をansatzと呼ぶ。 これを\(Z\)基底(computational basis)で測定すれば、各ビット列が観測され、サンプリングを繰り返すことで、確率(分布)を得ることができる。

このように量子ビットで波動関数(状態)\(\ket{\psi(\theta)}\)を作成したら、 次はハミルトニアンなどの演算子の期待値\(\bra{\psi(\theta)} H \ket{\psi(\theta)}\)を計算したくなる。

Variational Quantum Eigensolverは、

  1. 【Q】ansatz: 状態作成 (state preparation)の回路 \(\to \ket{\psi(\theta)}\)

  2. 【Q(C)】Hamiltonianの期待値 \(\bra{\psi(\theta)} H \ket{\psi(\theta)}\)を測定

  3. 【C】エネルギー(ハミルトニアンの期待値)を変分原理(やその他の条件)の下で最小化すべく\(\theta\)の最適化を行う

  4. 1-3までを収束するまで繰り返す

ことで、興味のある状態のエネルギーを推定しよう、というのが基本的な発想となる。 なお、1.-3.までに【Q】などを付したが、これはそれぞれの工程が"典型的には"量子(Q)/古典(C)計算機上で実行されることが 想定されている、という意味である。

このように、VQEでは量子・古典計算機の双方を駆使して問題を解くアプローチであり、これが良く量子-古典ハイブリッドと呼ばれる所以である。

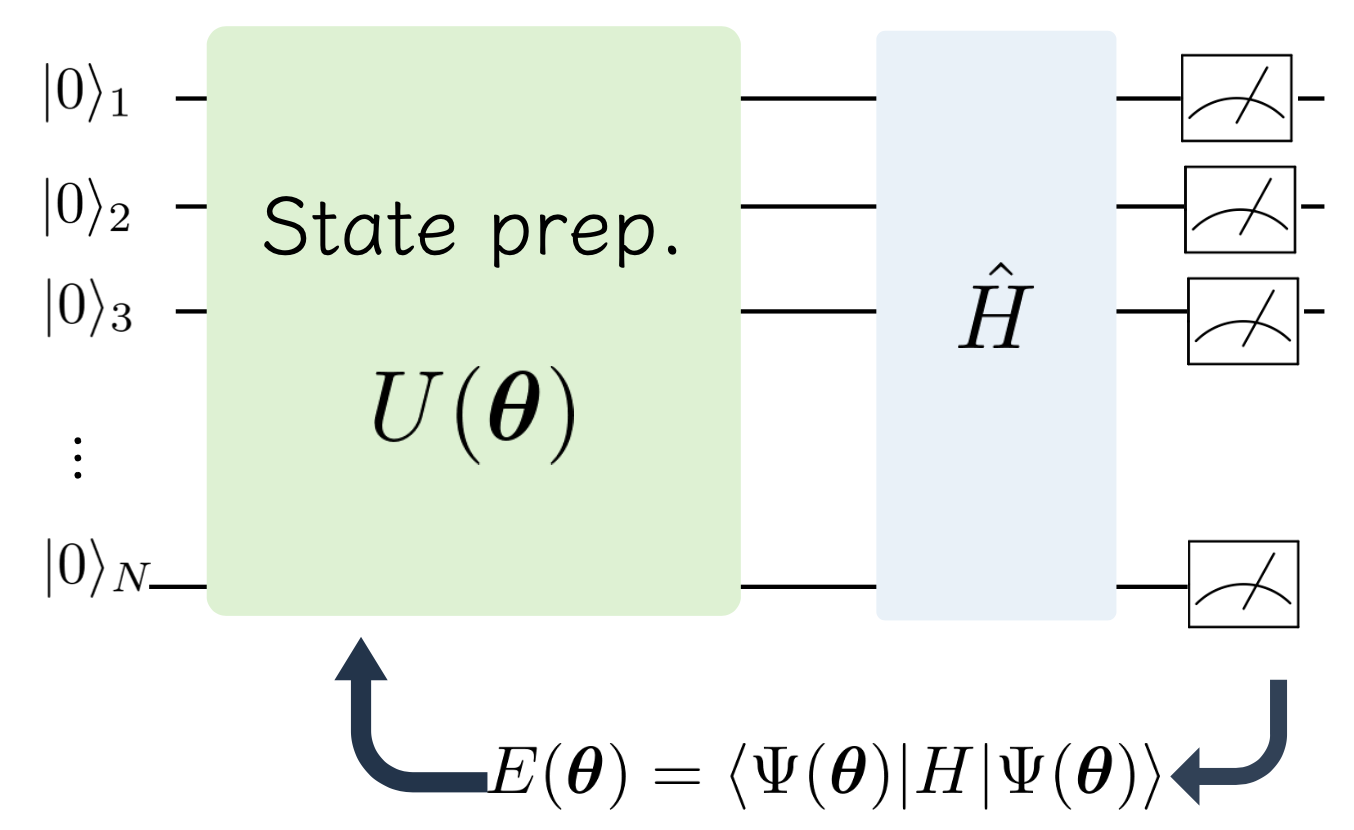
上ではハミルトニアン\(\hat{H}\)を一つのブロックとして描いたが、\( \langle \psi(\theta) | \hat{H} | \psi(\theta) \rangle\)を計算するためには、 各項の期待値を上の「演算子の期待値計算」のところで説明したように評価する必要がある。

9.5.2. Hadamard test/Quantum phase estimation (QPE)#

次に、long-term algorithmである量子位相推定(QPE)の説明を行う。

まず初めにHadamard testを紹介し、QPEの説明に移る。

9.5.2.1. Hadamard test#

アダマールテストは、1つの補助量子ビットを用いて興味のある系のユニタリ演算子の固有値を得る方法である。

以下では補助量子ビットのことをancilla、興味のある系を表現するための量子ビットをターゲット量子ビットと呼ぶことにする。 またターゲット量子ビットが既に、ユニタリ演算子\(U\)の固有状態である\(U\ket{\psi} = e^{i\lambda} \ket{\psi}\)とする。

Hadamard-gateとHamiltonianを混同しないようにしよう。 ここの節では、\(H\)はすべてH-gateを意味し、\(\hat{H}\)でHamiltonianを表現する。

Hadamard testの手順

  1. \(\ket{0}\)で初期化されたancillaに、H-gateを作用させる。

  2. ancillaを制御ビットとした、制御ユニタリ演算をターゲット量子ビットに作用させる。

  3. ancillaにH-gateを作用させ、その\(Z\)成分を測定する。

回路図にすると以下のようになる:

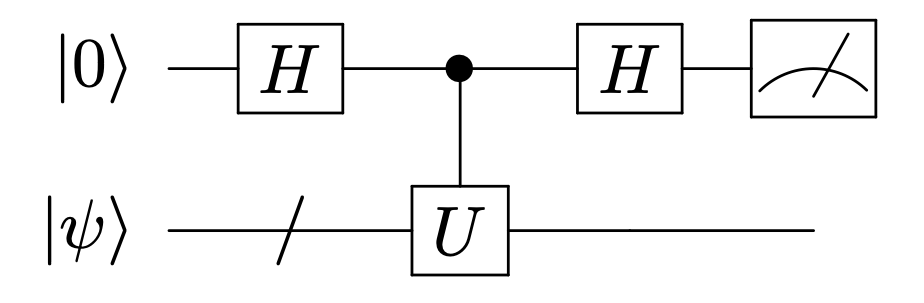
各ステップでの全系の状態を書き出してみよう。

\[\begin{split} \begin{align} 1. \quad & \frac{\ket{0}+\ket{1}}{\sqrt{2}} \otimes \ket{\psi} \\ 2. \quad & \frac{1}{\sqrt{2}} \ket{0} \otimes \ket{\psi} + \frac{1}{\sqrt{2}} \ket{1} \otimes U \ket{\psi}　\\ 3. \quad & \frac{\ket{0}+\ket{1}}{2} \otimes \ket{\psi} + \frac{\ket{0}-\ket{1}}{2} \otimes U \ket{\psi} \to \frac{1+e^{i \lambda}}{2} \ket{0} \otimes \ket{\psi} + \frac{1-e^{i \lambda}}{2} \ket{1} \otimes \ket{\psi} \end{align} \end{split}\]

すると、ancilla qubitを測定した結果が\(\ket{0}\)であるか\(\ket{1}\)であるかによって、 ユニタリ演算子の固有値の情報が引き出せる事がわかる。

\[\begin{split} \begin{align} P(0) & = \left| \frac{1+e^{i \lambda}}{2} \right|^2 = \frac{1+\cos \lambda}{2} \\ P(1) & = \left| \frac{1-e^{i \lambda}}{2} \right|^2 = \frac{1-\cos \lambda}{2} \end{align} \end{split}\]

実際に量子計算機でHadamard testを行う際は、ancillaに対する確率は、有限のshot数に対する\(0/1\)の割合となり近似が生じる。 系の固有値の古典計算が\(d=2^n\)の\(\mathcal{O}(d^3)\)程度とすると、 Hadamard testでは、必要な精度\(\epsilon\)に対して\(M \sim (1/\epsilon)^p\)回の測定が必要となる。

もし仮に、\(n\)個の量子回路に対する量子ゲート演算が古典計算より早くでき、ノイズも無視できるほどエラー低減/エラー訂正できれば、Hadamard testによって計算が高速化できる可能性がある。

Hadamard testを少し拡張すると、固有値を２進小数の各桁ごとに推定することができる。その工程を一度に行うのが、次に説明する量子位相推定(QPE)である。

9.5.2.2. Quantum phase estimation (QPE)#

次にQPEの概要を示す。 様々な拡張があるものの、最も代表的(教科書的)なQPEの説明にとどめておく。

ユニタリ演算子\(U\)とその固有ベクトル\(\ket{\psi}\)に対して、その固有値を求める事を考える。

(9.1)#\[ \begin{align} U \ket{\psi} = e^{i 2\pi\theta} \end{align} \]

上の\(\theta\)(位相)を求めることになる。また、より具体的な応用例として、量子系のエネルギーを推定したい場合には

\[\begin{split} \begin{align} U & = e^{ i\hat{H}t } \\ U \ket{\psi} & = e^{i\hat{H}t} \ket{\psi} = e^{iEt} \ket{\psi} \end{align} \end{split}\]

となる。ここで、\(\hat{H}\)は系のHamiltonian、\(E\)は系のエネルギー、\(t\)は時間(定数)である。 以下では、より一般の(9.1)の場合を考えよう。

QPEの手順

  1. \(n\)個のancilla \(\ket{A}\)を用意し、ターゲット量子ビットには\(\ket{\psi}\)を用意する。全系は\(\ket{\Psi} = \ket{A} \otimes \ket{\psi}\)とする。

  2. \(n_a\)個のancillaに対して、H-gateで重ね合わせ状態を作る。

  3. 各ancillaからターゲット量子ビットに制御ユニタリ演算子をそれぞれ\(U^{2^0}, U^{2^1}, \ldots, U^{2^{n_a-1}}\)回作用させる。

  4. (逆)量子フーリエ変換を施す。

  5. ancillaを測定する
    (2.のユニタリ演算の順番やどのancillaを上位ビットとするかはconventionに依る)。

  6. ancillaの測定結果から位相\(\theta\)を推定する。

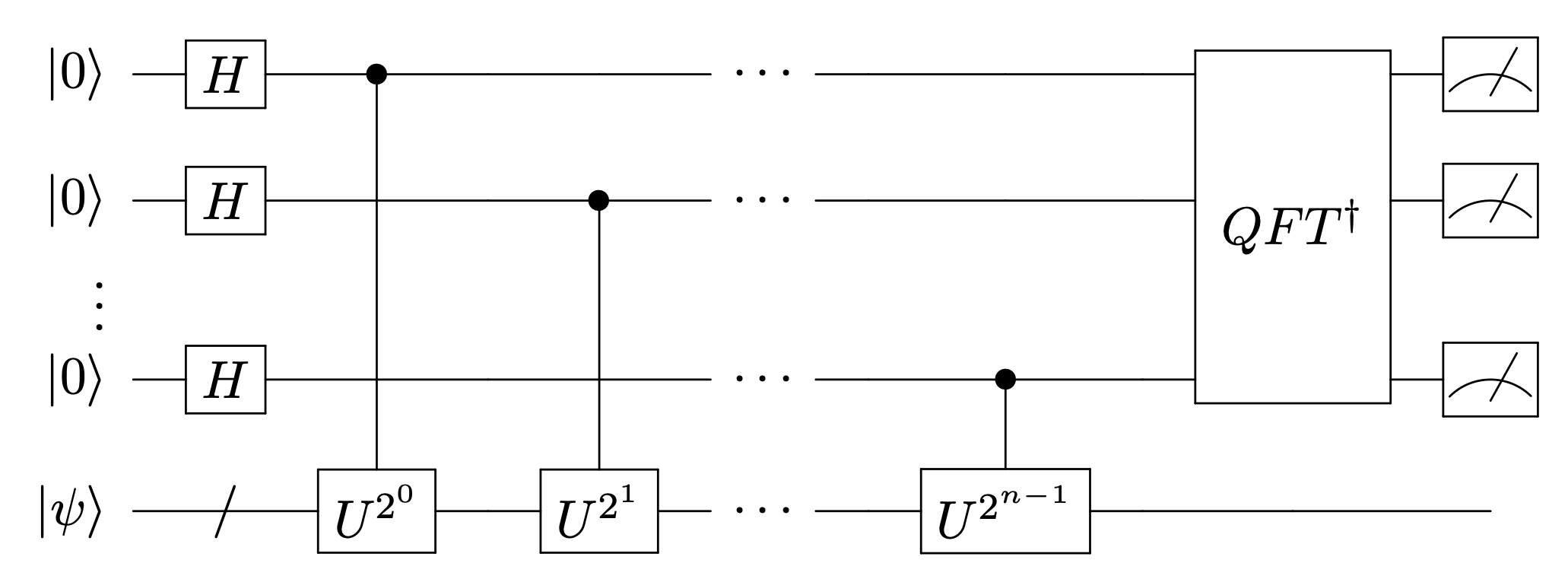
この回路によってなぜ固有値の推定ができるのかを見ていこう。

\[\begin{split} \begin{align} 1. & \to \ket{\Psi} = \ket{0}^{\otimes n} \otimes \ket{\psi} \\ 2. & \to \ket{\Psi} = \frac{1}{\sqrt{2^{n}}} \sum_{k=0}^{2^{n}-1} \ket{k} \otimes \ket{\psi} \\ 3. & \to \frac{1}{\sqrt{2^{n}}} \left[ \left( \ket{0} + e^{2\pi i \theta 2^0} \ket{1} \right) \otimes \left( \ket{0} + e^{2\pi i \theta 2^1} \ket{1} \right) \otimes \cdots \otimes \left( \ket{0} + e^{2\pi i \theta 2^{n-1}} \ket{1} \right) \right] \otimes \ket{\psi} \\ & = \frac{1}{\sqrt{2^{n}}} \sum_{k=0}^{2^{n}-1} e^{2\pi i \theta k} \ket{k} \otimes \ket{\psi} \\ 4. & \to \frac{1}{2^{n}} \sum_{k=0}^{2^{n}-1} \sum_{x=0}^{2^{n}-1} e^{2\pi i \theta k} e^{-2\pi i k x/2^n} \ket{x} \otimes \ket{\psi} \\ & = \frac{1}{2^{n}} \sum_{k=0}^{2^{n}-1} \sum_{x=0}^{2^{n}-1} e^{ -\frac{2\pi ik}{2^n}(x-2^n \theta) } \ket{x} \otimes \ket{\psi} \end{align} \end{split}\]

仮に\(2^n \theta\)が整数となるような \(\theta\)であったとすると、ancillaの値\(x\)を測定することで\(\theta\)を推定できることがわかる。 また、\(2^n \theta\)が整数でない場合も、\(x\)の測定結果は\(2^n \theta\)に近い値が高い確率で得られることが期待できるので、\(2\pi/2^n\)の精度で\(\theta\)を推定できる。

各ancilla qubitがレジスターになっており、位相の二進小数での各桁を担っている。 したがって、ancilla qubitを1つ追加するごとに、1bit分(10進数にして2)推定の精度を向上することができる。 もちろん様々な注がつくとはいえ、QPEでは、\(2\pi / 2^{n_a}\)の精度で固有値推定が可能であり、 仮にQPEに必要な量子ゲートの実行が高速で精度が十分であれば、古典計算に比べた量子計算の優位性が生じることになる。

試行波動関数について

Hadamard testやQPEに共通して想像される至極真っ当な疑問として、

「計算が大変な系の波動関数やエネルギーを推定したいのに、ターゲット量子ビットで既に目的となる波動関数が用意されていることが前提になっているではないか。それをどうやって用意するんだ！？」

という疑問が生じるかと思う。 QPEでは、必ずしも\(\ket{\psi}\)はターゲット系の厳密解であることは要請されない。 目的となる厳密解と有限のオーバーラップを持っていれば良い。

試行波動関数を、(知り得ない)真の波動関数で展開するとわかるように 興味のある固有値を測定できる確率は、真の波動関数とのoverlap amplitudeに比例するため、 できるだけ良い試行波動関数を使わなければならない、というのは事実としてある。

そこでHFやBCS, CC, truncateされた空間でのCI波動関数, あるいはVQEで最適化した範囲でのansatzなど、 状況に応じて(様々なトレードオフで)QPEのinputを選ぶことになるだろう。 いずれにしても、QPEはQFT自体がlong-term algorithmであること、 制御ユニタリ演算など必要な回路が非常に深くなること、 ターゲット量子ビットの状態作成の非自明さ・コスト、実機におけるエラー率などから、 古典計算機の適用限界を超えた計算は2025年8月現在においては非常に難しい。

しかしながら、幾つかの(期待も含めた？)条件のもとで、量子コンピュータの優位性が期待されている 量子アルゴリズムの一つであることは間違いない。

また、long-termアルゴリズムの検討と平行する形で、限られたリソース(qubit)やエラー率のなかでのNISQデバイスを用いた計算の工夫が、 量子多体系に対する新たな量子アルゴリズムの提案に繋がってきたことも強調したい。

9.6. Python framework for Quantum Computing#

Pythonで量子計算を行うためのフレームワークはいくつかあるが、ここでは筆者が使用経験のあるものを紹介する。 特徴などの説明については、あくまで筆者の非常に限られた経験と浅い理解に基づくもので誤りである可能性は大いにあることは断っておく。 また、その際は、そっと教えていただけると幸いである。 回路やオペレータ表現についてフレームワーク間を行き来する互換機能なども其々のフレームワークに用意されていたりもするが、 ソフトウェア面においても発展が急速すぎるため、必ずしもうまく行き来できるとは限らない。

したがって、(とくに実機利用を行う場合には)自身の解きたい問題や使いたいハードウェアにあわせて、フレームワークを選択することが重要であると同時に、 計算を行った際の仮想環境・ライブラリのバージョン情報などは保持しておこう。

  • Qiskit (IBM) 言わずとしれた、IBMが開発している量子計算用のPythonフレームワーク。
    2024年2月のメジャーバージョンアップデート以降、APIやDocumentが大幅に破壊的な変更を受け、古いコードが動かないことが多い。 筆者は大変困っていてやや脱落気味であるが、この資料作成にあたって力を振り絞り、Qiskitを使った実装例も示すことにした。 Qiskit1.0チートシートなど、有志による情報も参考になる。

  • Pennylane (Xanadu) 量子計算と機械学習を統合したフレームワーク。
    OpenFermionとの連携が強く、量子化学計算などで用いられる実装が利用できる他、量子機械学習のアルゴリズムも実装されている(筆者は使ったことがない)。 量子化学の計算に関するTutorialもあるなど、量子多体系への適用の障壁はやや低い印象。 また、いろいろなタッチの回路を描くことができる。

  • pytket (Quantinuum) Quantinuum社が開発している量子計算用のPython モジュール。筆者は絶賛勉強中。
    Trotter分解、制御ユニタリ演算の構築などの、物理系のシミュレーションに不可欠なハミルトニアンの時間発展に関する実装はやや未整備な印象。

続く章で３つのフレームワークを用いた簡単な量子計算の実装例を示すが、(少なくともsimulatorレベルでは)pennylaneが最も使いやすい印象を受けた。 とくに、制御ユニタリ/ハミルトニアンの時間発展や、QPEの実装がよく整備されており、興味のある系に応用しやすいであろう。

それぞれの章では、フレームワークの得手不得手(や筆者の理解)によって、以下の表のように、少しずつ異なるトピックを扱った。

フレームワーク

VQE

回路パラメータの最適化

Hadamar test

QPE

Quantum Krylov

Pennylane

◯

◯※1

◯

◯

-

Qiskit

◯

-

◯

◯

◯

pytket

◯

◯※2

-

-

-

9.7. その他の注#

この資料では、いずれの計算においてもStatevectorか、Aerのノイズfreeなsimulatorを用いる計算結果を示し、実機へのジョブの投げ方などは扱っていない。 simulatorという際、何を指しているのかが初学者に分かりづらい事がある(筆者もそうだった)が、この資料では以下のように使い分けている。 Statevectorは回路に基づいて全ての状態を陽に計算する方法であり(したがって回路にmeasurementを入れてはいけない)、当然ながら、qubit数が増えると指数関数的に計算量が増える。 "shotで測る"などと言う際は、回路の終端で量子ビットの状態を測定する。1回の測定で得られるのは、確定的な1つのビット列である。 これを繰り返してサンプリングし、ビット列の出現回数から確率を推定する方法を指す。 ノイズが無い場合でも、statevectorよりも、実機での実行を見越した方法になっているが、統計誤差が生じることに注意が必要である。

他にも、実機で計算を行う際は、それ専用のおまじないを理解する必要がある上、 意味のある結果を得るためには、エラー抑制(error mitigation)やpost-processingなど重要なステップが必要となるが、 これらについてはこの資料の範囲外とすることを了承いただきたい。