1. pairing Hamiltonian

この章では、資料を通して扱うことになるpairing Hamiltonianについて説明する。

1.1. Hamiltonian

核子系はさらに多体相互作用を持つ特徴ある量子多体系である。

一般の一体・二体相互作用する系のHamiltonianは、一体部分\(T\)と相互作用部分\(V\)に分けて書ける。

\[ \begin{align} H = \sum_{ij} h_{ij} a^{\dagger}_i a_j + \frac{1}{4} \sum_{ijkl} v_{ijkl} a^{\dagger}_i a^{\dagger}_j a_l a_k \equiv T + V \end{align} \]

なかでも本講義では、２重に縮退したエネルギー準位を持つ\(N\)個の粒子系を考える。例えば電子spinのup/downが縮退している場合などに相当する。 またそれぞれの粒子は、同一準位に２個粒子が占有されているときのみに働くペアリング相互作用を持っているとすると、 系のハミルトニアンは下記のように書き下せる。

(1.1)\[ \begin{align} H_\mathrm{pair} = \sum_{i=1}^{N} \epsilon_i a_i^\dagger a_i - \frac{g}{4} \sum_{ij} a_i^\dagger a^\dagger_{\bar{i}} a_{\bar{j}} a_j \end{align} \]

以降特に断りなくハミルトニアン(Hamiltonian)と呼ぶ際には、(1.1)を指すことにする。

ここで、\(\epsilon_i\)は\(i\)番目の一粒子エネルギー, \(g\)は相互作用定数, \(a_i^\dagger\)は\(i\)番目の粒子を生成する演算子、\(a_i\)は\(i\)番目の粒子を消滅させる演算子である。 また、資料内で適宜globalなといった表現をすることがあるが、相互作用の強さが\(jj\)-couplingの軌道角運動量\(j\)に依存したりするものとの対比で用いている。

続く以下の章では、様々な多体計算手法を用いてこの系の基底状態を計算することになる。この形ですべての手法について議論しても良いが、議論と実装を簡単にするために、偶数個の粒子の場合に限定し、Fermion１粒子の演算子を２つセットにした、ペア生成・消滅演算子, ペア数演算子についても導入することにしよう。

\[ P^{\dagger}_p \equiv a^{\dagger}_p a^{\dagger}_{\bar{p}}, \quad P_p \equiv a_{\bar{p}} a_p, \quad N_p \equiv a^{\dagger}_p a_p + a^{\dagger}_{\bar{p}} a_{\bar{p}} \]

ここで、\(\bar{p}\)は\(p\)に対応するペアの(元の表示での)indexである。 右辺では元の１粒子軌道のindex, 左辺ではペアのindexが同じ\(p\)で表現されていることに注意。 元の演算子がFermionの反交換関係を満たすのに対し、ペア生成・消滅演算子、ペアの数演算子は次のような交換関係を満たす。

\[\begin{split} \begin{align} [ P_{p}, P^{\dagger}_{q} ] &= \delta_{pq} (1 - N_{p}) \\ [ N_{p}, P^{\dagger}_{q} ] &= 2 P^{\dagger}_{p} \delta_{pq} \\ [ N_{p}, P_{q} ] &= -2 P_{q} \delta_{pq} \end{align} \end{split}\]

この粒子対による表示のもとでは、Hamiltonianは次のように書き換えられる。

\[ H = \sum_{p} \epsilon_p N_p - g \sum_{pq} P^{\dagger}_p P_q \]

元の二体項の和は\(m = \pm 1/2\)について取る一方で\(pq\)は何れかについて取るため、1/4の因子が消えることに注意。 下に、今考えている系と、上で行った変換の模式図を示した。

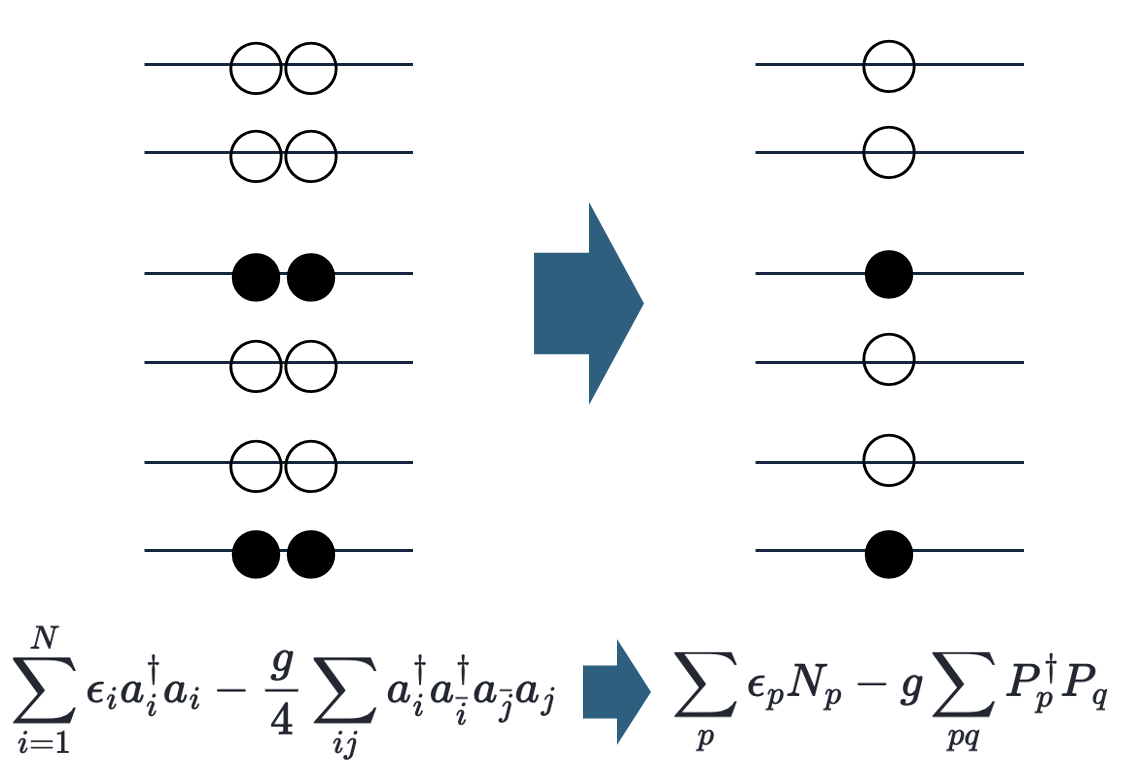
奇数粒子の系や、異なるエネルギー準位の粒子が混ざる場合(ペアリング以外の相互作用)には、一般にこの表現は使えないが、 Full-CI法と量子計算の章では、この表現を用いることにする。 これにより、必要な軌道(または量子ビット)の数が半分にできるため、要求リソースが高い手法や量子計算等の場合には重要な工夫となる。

各多体計算手法の説明をする前に、模型の意味を解説するために結果をプロットしておこう。

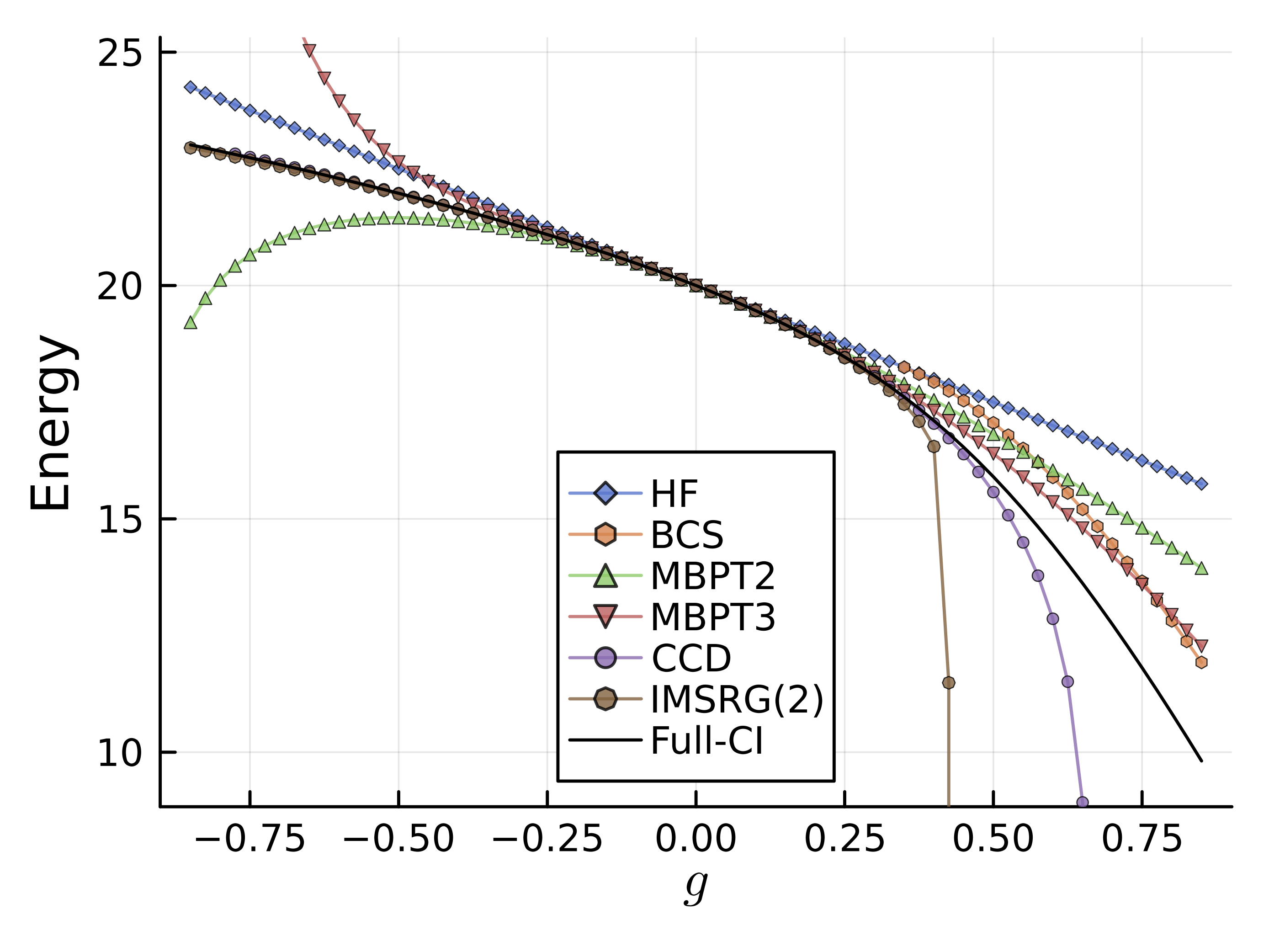
ペアリングの強さ\(g\)が0の場合、エネルギーは下の順位から詰めていった場合のエネルギーと等しくなる。 \(g\)が負の大きな値を取ると, 上の式の第二項の寄与は斥力的に働く。 \(g\)が正の大きな値を取ると、第二項の寄与は引力的に働き, 第1項と競合し始める。 ある臨界値を超えると、ペアリングが優勢となり\(g \to \infty\)の極限で, 個々の一粒子軌道は区別できなくなり,ある種の超流動状態が形成される。

1.2. 発展的な注

1.2.1. 実装上の注: 波動関数の反対称化について

一般のCI計算でHamiltonianによる遷移行列要素を求める際には、operatorの並び順を考慮してきちんと(反)対称化する必要がある。

例えば、\(a^{\dagger}_i a^{\dagger}_j a_k a_l\)と\(a^{\dagger}_i a^{\dagger}_j a_l a_k\)の それぞれにひっつく相互作用の係数は、全体として適切な対称性を担保していなければならない。 よりgeneralな(例えばHO基底での)相互作用の場合、こうしたphase/factorを相互作用ファイルに持たせるのか、 redundantな項は書き出さず、特定のindexの並びについてのみ相互作用の係数を書き出しておいて、 CG係数やphase/factorなどは実際の計算コードの中で考慮にいれるのかなど、詳細について理解しておく必要がある。

pairing Hamiltonianの場合、indexの入れ替えで余計なお釣りが発生しないことを積極的に用いて実装を簡略化してある。

1.2.2. pairing Hamiltonianの拡張

上で考えたpairing Hamiltonianは、グローバルパラメータ\(g\)を一つ持つだけの、最も簡単な例である。

より現実の核子系を記述することを目的として、様々な拡張も考えられてきた。

最も単純な拡張は、軌道角運動量に依存する相互作用を考えることである。

\[ \begin{align} H = \sum_{j,m} \epsilon_j n_{jm} - \sum_{j,j'} \sum_{m>0} \sum_{m'>0} G_{jj'} a^{\dagger}_{jm} \tilde{a}^{\dagger}_{jm} \tilde{a}_{j'm'} a_{j'm'} \end{align} \]

あるいは、核子対の合成角運動量に対する依存性から以下のような相互作用を考えることもできる。

\[ \begin{align} H = \sum_{j,m} \epsilon_j n_{jm} -\frac{1}{4} \sum_{J} \sum_{jj'} G^J_{jj'} \sum_M \sum_{mm'nn'} C^{JM}_{jmjn} C^{JM}_{j'm'j'n'} a^{\dagger}_{jm} a^{\dagger}_{jn} a_{j'n'} a_{j'm'} \end{align} \]