10. pennylaneを用いたVQE計算#
import numpy as np
import itertools
from itertools import combinations
import matplotlib.pyplot as plt
10.1. Hamiltonianの準備#
pairing Hamiltonianは以下のように書ける:
\[
H = \sum_{p} \epsilon_p N_p - g \sum_{pq} P^{\dagger}_p P_q
\]
\(p,q\)は二重縮退した軌道のラベルであり、\(N_p\)は数演算子である。 \(P^{\dagger}_p\), \(P_p\)はそれぞれ軌道\(p\)にペアの粒子を生成/消滅する演算子である。
以下ではまずペアリングハミルトニアンの行列要素を計算するためのクラスを定義しておく。
Show code cell source
class PairingHamiltonian:
def __init__(self, Norb, Nocc, gval, delta_eps=1.0):
self.Norb = Norb
self.Nocc = Nocc
self.delta_eps = delta_eps
self.gval = gval
self.basis = self.make_basis()
self.epsilon = self.eval_epsilon()
self.Hmat = self.eval_Hmat()
def make_basis(self):
self.basis = []
for occ in combinations(range(self.Norb), self.Nocc):
self.basis.append(occ)
return self.basis
def eval_epsilon(self):
self.epsilon = [ 2 * i * self.delta_eps for i in range(self.Norb) ]
return self.epsilon
def eval_Hmat(self):
dim = len(self.basis)
self.Hmat = np.zeros((dim, dim))
for bra_idx, bra in enumerate(self.basis):
for ket_idx, ket in enumerate(self.basis):
# Hamming distance
diff = [ i for i in bra if i not in ket ]
same = [ i for i in bra if i in ket ]
# for SPE term
if bra_idx == ket_idx:
self.Hmat[bra_idx, ket_idx] += np.sum( [self.epsilon[i] for i in same])
self.Hmat[bra_idx, ket_idx] += - self.gval * len(same)
# for pairing term
if len(diff) == 1:
self.Hmat[bra_idx, ket_idx] = - self.gval
return self.Hmat
def tuple_to_bitstring(tup, Norb, rev=True):
bitint = 0
for i in tup:
bitint += 2**i
if rev:
bitstring = "|"+format(bitint, f'0{Norb}b')[::-1]+">"
else:
bitstring = "|"+format(bitint, f'0{Norb}b')+">"
return bitstring
Norb = 4
Nocc = 2
gval = 0.33
Hamil = PairingHamiltonian(Norb, Nocc, gval)
evals, evecs = np.linalg.eigh(Hamil.Hmat)
evals = np.linalg.eigvalsh(Hamil.Hmat)
Egs_exact = evals[0]
E_HF = Hamil.Hmat[0,0]
print("basis:", Hamil.basis)
print([tuple_to_bitstring(tup, Norb) for tup in Hamil.basis])
print("eps: ", Hamil.epsilon)
print("Hmat: ", Hamil.Hmat)
print("evals: ", evals)
print("Egs_exact: ", Egs_exact, " E_HF", E_HF)
print("gs evec", evecs[:,0])
print("gs prob", evecs[:,0]**2)
basis: [(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
['|1100>', '|1010>', '|1001>', '|0110>', '|0101>', '|0011>']
eps: [0.0, 2.0, 4.0, 6.0]
Hmat: [[ 1.34 -0.33 -0.33 -0.33 -0.33 0. ]
[-0.33 3.34 -0.33 -0.33 0. -0.33]
[-0.33 -0.33 5.34 0. -0.33 -0.33]
[-0.33 -0.33 0. 5.34 -0.33 -0.33]
[-0.33 0. -0.33 -0.33 7.34 -0.33]
[ 0. -0.33 -0.33 -0.33 -0.33 9.34]]
evals: [1.18985184 3.29649666 5.34 5.34 7.42853393 9.44511758]
Egs_exact: 1.1898518351360725 E_HF 1.3399999999999999
gs evec [0.97121327 0.18194077 0.09817385 0.09817385 0.06360816 0.01789242]
gs prob [9.43255208e-01 3.31024447e-02 9.63810492e-03 9.63810492e-03
4.04599822e-03 3.20138762e-04]
10.2. pennylaneを用いた表現#
上では、(many-body)basisに対して行列要素を計算しているが、 実際に量子計算を行う際には、Hamiltonianを第二量子化された演算子の形で扱う方が便利である。 より具体的には、演算子と、それに付随する係数の形でHamiltonianを表現する。
以下では、pennylaneを用いた表現でHamiltonianを定義してみよう。 pennylaneはXanaduの提供する量子計算ライブラリであり、その開発経緯もあり、OpenFermionやPyTorchとの連携が強い。 したがって、量子化学計算や量子機械学習について既存の資産(≒実装)を活用することができる。 pennlaneはよくqmlとしてimportされるが、これはQuantum Machine Learningの略のようだ。
pennylaneを用いる際の注意点としては、pennylane内のnumpyを使うこと。
import pennylane as qml
from pennylane import numpy as np
import openfermion as of
勾配の計算などを効率的に行えるようにだろうか、配列をTorchTensorにしているようだ:
np.array([1.0])
tensor([1.], requires_grad=True)
OpenFermionのメソッドを用いて、演算子のプールを作ってみよう。
def ij_tuple_to_AdagA_str(tuple_in):
i, j = tuple_in
return f"{i}^ {j}"
SPEs = Hamil.epsilon
H_op = of.ops.FermionOperator()
for i in range(Hamil.Norb):
op_key = ij_tuple_to_AdagA_str((i,i))
H_op += of.ops.FermionOperator(op_key, SPEs[i])
for i in range(Hamil.Norb):
for j in range(Hamil.Norb):
op_key = ij_tuple_to_AdagA_str((i,j))
H_op += of.ops.FermionOperator(op_key, -Hamil.gval)
print("Hamiltonian operators\n", H_op, sep="")
Hamiltonian operators
-0.33 [0^ 0] +
-0.33 [0^ 1] +
-0.33 [0^ 2] +
-0.33 [0^ 3] +
-0.33 [1^ 0] +
1.67 [1^ 1] +
-0.33 [1^ 2] +
-0.33 [1^ 3] +
-0.33 [2^ 0] +
-0.33 [2^ 1] +
3.67 [2^ 2] +
-0.33 [2^ 3] +
-0.33 [3^ 0] +
-0.33 [3^ 1] +
-0.33 [3^ 2] +
5.67 [3^ 3]
次に、これを量子コンピュータ上で計算するためのmappingを行う。 通常、フェルミ粒子の多体系では、Jordan-Wigner変換やBravyi-Kitaev変換を用いてマッピングするが、 Pairing Hamiltonianの場合は、JWで出てくる反交換関係を保つためのお釣りが無視できて、シンプルな表式になる。
\[\begin{split}
\begin{align}
P^{\dagger}_p & = \frac{1}{2} (X_p - iY_p) \\
P_p & = \frac{1}{2} (X_p + iY_p) \\
N_p & = \frac{1}{2} ( 1 - Z_p) \\
H & = \sum_{p} \epsilon_p N_p - g \sum_{pq} P^{\dagger}_p P_q \\
& = \sum_{p} \epsilon_p \frac{1}{2} ( 1 - Z_p) - g \sum_{pq} \frac{1}{4} (X_p - iY_p)(X_q + iY_q) \\
& = \sum_{p} \frac{\epsilon_p - g}{2} (1 - Z_p ) - \frac{g}{4} \sum_{p \neq q} (X_pX_q + Y_pY_q) \\
\end{align}
\end{split}\]
SPEs = Hamil.epsilon
obs = [ ]
coeffs = [ ]
# 1-Zp term
for i in range(Hamil.Norb):
op = qml.Identity(i) - qml.PauliZ(i)
obs += [ op ]
coeffs += [ 0.5 * (SPEs[i] - Hamil.gval) ]
# XX+YY term
for i in range(Hamil.Norb):
for j in range(i+1, Hamil.Norb):
if i == j:
continue
factor = - Hamil.gval / 2
XX = qml.PauliX(i) @ qml.PauliX(j); obs += [ XX ]; coeffs+= [ factor ]
YY = qml.PauliY(i) @ qml.PauliY(j); obs += [ YY ]; coeffs+= [ factor ]
H_qubit = qml.Hamiltonian(coeffs, obs)
H_qubit
(
-0.165 * (I(0)
+ -1 * Z(0))
+ 0.835 * (I(1)
+ -1 * Z(1))
+ 1.835 * (I(2)
+ -1 * Z(2))
+ 2.835 * (I(3)
+ -1 * Z(3))
+ -0.165 * (X(0) @ X(1))
+ -0.165 * (Y(0) @ Y(1))
+ -0.165 * (X(0) @ X(2))
+ -0.165 * (Y(0) @ Y(2))
+ -0.165 * (X(0) @ X(3))
+ -0.165 * (Y(0) @ Y(3))
+ -0.165 * (X(1) @ X(2))
+ -0.165 * (Y(1) @ Y(2))
+ -0.165 * (X(1) @ X(3))
+ -0.165 * (Y(1) @ Y(3))
+ -0.165 * (X(2) @ X(3))
+ -0.165 * (Y(2) @ Y(3))
)
10.3. HF状態の準備と測定#
def call_HF(occupied, ret="H"):
for i in occupied:
qml.PauliX(wires=i)
if ret == "H":
return qml.expval(H_qubit)
elif ret == "Z":
return np.array([ qml.sample(qml.PauliZ(i)) for i in range(Norb)])
elif ret == "state":
return qml.state()
dev = qml.device("default.qubit", wires=Norb)
@qml.qnode(dev)
def circuit(occupied, ret="H"):
return call_HF(occupied, ret)
for occupied in [[0, 1], [0,2], [1,2], [0,3], [1,3], [2,3]]:
E_HF = circuit(occupied)
print("occ. ", occupied, "E_HF: ", E_HF)
print("あってるかチェック... Hmat_diag. ", np.diag(Hamil.Hmat))
occ. [0, 1] E_HF: 1.3399999999999999
occ. [0, 2] E_HF: 3.34
occ. [1, 2] E_HF: 5.34
occ. [0, 3] E_HF: 5.34
occ. [1, 3] E_HF: 7.34
occ. [2, 3] E_HF: 9.34
あってるかチェック... Hmat_diag. [1.34 3.34 5.34 5.34 7.34 9.34]
10.4. 回路によるEnergy測定と最適化#
以下では、実際に回路を用いてエネルギーを測定しつつ、(statevectorを使って、という条件付きだが)回路パラメータの最適化も行う。
やはりここでも注意しないといけないのが、回路のパラメータもpennylane内のnumpyを使って、TorchTensorで与える必要がある。 最適化すべき角度のパラメータをリストで与えると最適化が進まない。
params_exact = np.array([-0.48104276, -1.03976498, -0.98963981, -1.18481738, -0.54832984] )
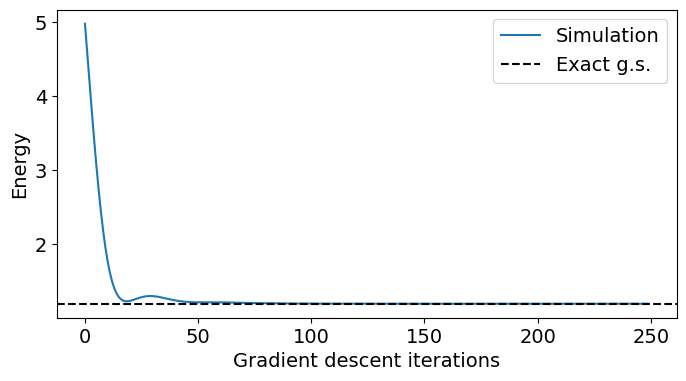
def plot_Energy_Opt(energies):
plt.rcParams["font.size"] = 14
plt.figure(figsize=(8, 4))
plt.plot(energies, label="Simulation")
# for eval in evals:
# plt.axhline(y=eval, color="gray", linestyle="dotted")
plt.axhline(y=Egs_exact, color="black", linestyle="dashed", label="Exact g.s.")
plt.xlabel("Gradient descent iterations")
plt.ylabel("Energy")
plt.legend()
plt.show()
def call_ansatz(params, ret="H"):
for i in range(Nocc):
qml.PauliX(wires=i)
qml.SingleExcitation(params[0], wires=[1,2])
qml.SingleExcitation(params[1], wires=[2,3])
qml.ctrl(qml.SingleExcitation, control=[2])(params[2], wires=[0,1])
qml.ctrl(qml.SingleExcitation, control=[3])(params[3], wires=[0,1])
qml.ctrl(qml.SingleExcitation, control=[3])(params[4], wires=[1,2])
if ret == "H":
return qml.expval(H_qubit)
elif ret == "Z":
return np.array([ qml.sample(qml.PauliZ(i)) for i in range(Norb)])
elif ret == "state":
return qml.state()
def make_angle_to_0_2pi(angle):
return angle % (2 * np.pi)
dev = qml.device("default.qubit", wires=Norb)
@qml.qnode(dev)
def ansatz(params):
return call_ansatz(params, "H")
# Specifying the initial parameters
num_params = 5
np.random.seed(11)
params = np.random.uniform(-np.pi, +np.pi, num_params)
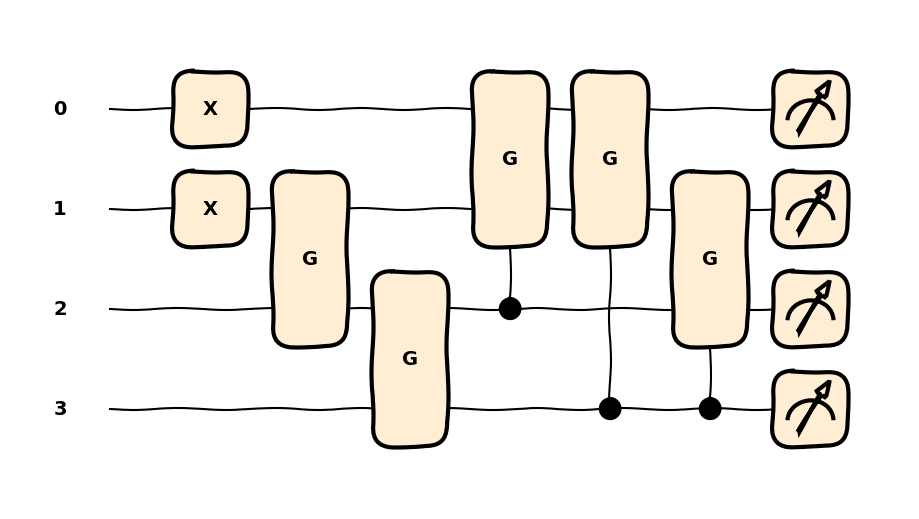
# Drawing the circuit
style="sketch"
qml.drawer.use_style(style)
fig, ax = qml.draw_mpl(ansatz)(params)
plt.show()
plt.close()
# Calculating the energy
E = ansatz(params)
print("Initial guess\nE", E, "Egs_exact", Egs_exact, "Diff.", E - Egs_exact)
# Optimizing parameters (not working)
if True: #False:
N_its = 250
energies = []
optimizer = qml.AdamOptimizer(stepsize=1.e-1)
for _ in range(N_its):
params, _cost = optimizer.step_and_cost(ansatz, params)
energies.append(_cost)
plot_Energy_Opt(energies)
E = ansatz(params)
print("Optimized\nE", E, "Egs_exact", Egs_exact, "Diff.", E - Egs_exact)
print("params Opt (0~2π): ", params.tolist())
print("params_exact(0~2π):", params_exact.tolist())
Initial guess
E 4.977989165302643 Egs_exact 1.1898518351360725 Diff. 3.7881373301665704
Optimized
E 1.1898518352304182 Egs_exact 1.1898518351360725 Diff. 9.434564240962118e-11
params Opt (0~2π): [-0.4810427640772028, -1.0397649774759907, -0.9896398067194048, -1.1848173802177666, -0.5483298352025293]
params_exact(0~2π): [-0.48104276, -1.03976498, -0.98963981, -1.18481738, -0.54832984]
うまく回路パラメータの最適化もできて、厳密解を再現できた。
ここまではstatevector(状態作成した結果の配列を直接持つ)を用いたが、デバイスの設定でshot数を設定すると、statevectorではなく、結果の統計を得ることができる。
def sample_to_counts(sample):
n_qubits, n_shots = np.shape(sample)
sample_bin = (1-np.array(sample))/2
dict_counts = { }
for i in range(n_shots):
label = ''.join([str(int(sample_bin[j,i])) for j in range(n_qubits)])
dict_counts[label] = dict_counts.get(label, 0) + 1
return dict_counts
dev = qml.device("default.qubit", wires=range(Norb), shots=10000)
@qml.qnode(dev)
def ansatz(params):
return call_ansatz(params, "Z")
config_ordered = [ ]
for config in itertools.combinations(range(Norb),Nocc):
config_ordered += [f'{sum([2**i for i in config]):0{Norb}b}']
labels = sorted(config_ordered,reverse=True)
counts = sample_to_counts(ansatz(params))
values = [ ]
for config in labels:
values.append(counts.get(config, 0))
values = np.array(values) / np.sum(values)
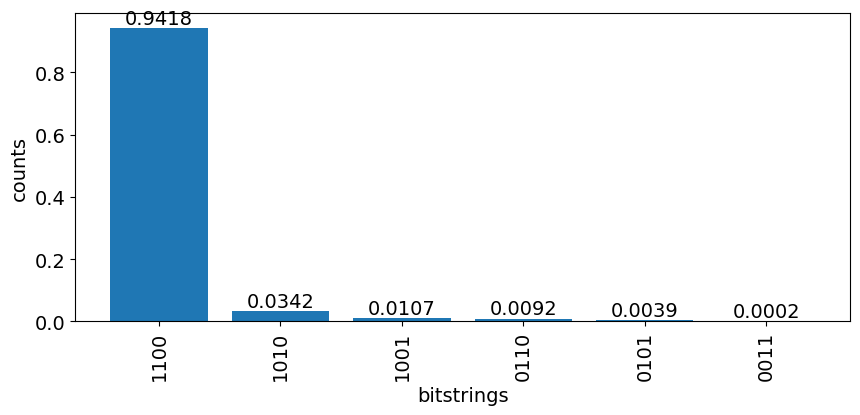
fig = plt.figure(figsize=(10, 4))
plt.bar(labels,values)
for i in range(len(labels)):
plt.text(i, values[i], str(values[i]), ha='center', va='bottom')
plt.xlabel('bitstrings')
plt.ylabel('counts')
plt.xticks(rotation=90)
plt.show()
plt.close()
# Checking the state-vector
dev = qml.device("default.qubit", wires=range(Norb))
@qml.qnode(dev)
def ansatz(params):
return call_ansatz(params, "state")
ansatz(params)
tensor([0. +0.j, 0. +0.j, 0. +0.j, 0.01788929+0.j,
0. +0.j, 0.06360699+0.j, 0.09817351+0.j, 0. +0.j,
0. +0.j, 0.09817219+0.j, 0.18193914+0.j, 0. +0.j,
0.97121391+0.j, 0. +0.j, 0. +0.j, 0. +0.j], requires_grad=True)
10.5. 補足#
pennylaneでは標準のバックエンドdev = qml.device("default.qubit", wires=n_qubits)に加えて、
C++による高速なstatevectorのシミュレーションが可能なバックエンドも用意されている。
dev = qml.device("lightning.qubit", wires=n_qubits)
などとしてやれば良い。