ベイズ線形回帰#
線形回帰 (多項式回帰の例)#
線形回帰モデル:
\(y({\bf x},{\bf w})= \sum^{M-1}_{j=0} w_j \phi_j({\bf x}) = {\bf w}^T\boldsymbol{\phi}({\bf x})\)を考える。
ここで\(\boldsymbol{\phi}\)は基底関数のベクトルで、 \(p\)次の多項式回帰の場合は\(\boldsymbol{\phi}=(1, x, x^2, \ldots, x^p)\)といった感じ。
実際この場合にベクトルの内積を書き下すと \({\bf w}^T\boldsymbol{\phi}=w_0 + w_1x+ w_2x^2+ \cdots + w_{p}x^p\)となり、 \(p\)次多項式になっている。
さて目標変数\(t\)が、決定論的な関数\(y({\bf x},{\bf w})\)と平均0,精度\(\beta\equiv 1/\sigma^2\)の誤差\(\epsilon\)の和: \(t=y({\bf x},{\bf w})+\epsilon\)で与えられていると仮定する。
つまり、\(t\)の確率分布が \(p(t|{\bf x},{\bf w},\beta) = \mathcal{N}(t|y({\bf x},{\bf w}),\beta^{-1})\)で与えられるとする。
入力\(\boldsymbol{\mathrm{X}}=\{{\bf x_1},{\bf x_2},\ldots, {\bf x_N}\}\)と、 対応する目標値を\(\boldsymbol{\mathrm{t}}=\{t_1,t_2,\ldots, t_N\}\)と表すことにしておこう。
これらのデータ点が上の分布\(p(t|{\bf x},{\bf w},\beta)\)から独立に生成されたと仮定すると、
データの目標変数についての確率分布は\(p(\boldsymbol{\mathrm{t}}|\boldsymbol{\mathrm{X}},{\bf w},\beta) = \prod^N_{n=1} \mathcal{N}(t_n|{\bf w}^T \boldsymbol{\phi}({\bf x_n}) ,\beta^{-1})\)で与えられる。
(以下では、確率分布の条件部分にある\({\bf x}\)などを適宜省略する)
このとき、対数尤度は \(\ln p(\boldsymbol{\mathrm{t}}|{\bf w},\beta) = \sum^N_{n=1} \ln \mathcal{N}(t_n|{\bf w}^T\boldsymbol{\phi}({\bf x_n}) ,\beta^{-1}) = \frac{N}{2}\ln\beta - \frac{N}{2}\ln(2\pi) -\beta E_D({\bf w})\)となる。
なお\(E_D\)は二乗和誤差関数: \(E_D({\bf w}) \equiv \frac{1}{2}\sum^N_{n=1} \{ t_n- {\bf w}^T \boldsymbol{\phi}({\bf x_n}) \}\) である。
対数尤度の勾配を書き下して、最尤推定を考えるとすると\(\nabla \ln p(\boldsymbol{\mathrm{t}}|{\bf w},\beta) = \beta \sum^N_{n=1} \{ t_n -{\bf w}^T \boldsymbol{\phi}({\bf x_n}) \} \boldsymbol{\phi}({\bf x_n})^T \)の根が必要。
つまり\(0= \sum^N_{n=1} t_n \boldsymbol{\phi}({\bf x_n})^T - {\bf w}^T(\sum^N_{n=1}\boldsymbol{\phi}({\bf x_n})\boldsymbol{\phi}({\bf x_n})^T)\)をときたい。
上の式を変形すると\({\bf w} = ( \boldsymbol{\Phi}^T\boldsymbol{\Phi} )^{-1} \boldsymbol{\Phi}^T \boldsymbol{\mathrm{t}}\)が根であることがわかる。
つまり、最尤推定を与えるパラメータ\({\bf w}_{ML}\)は、計画行列\(\boldsymbol{\Phi}\)を用いて閉じた形で与えられる。
なお、計画行列の要素は \(\boldsymbol{\Phi}_{nj} = \phi_j({\bf x_n})\)で与えられる。
次の1次元擬似データの回帰を考えてみる。
import numpy as np
from matplotlib import pyplot as plt
## データ点の生成
np.random.seed(1234)
x = np.linspace(-2.0,6.0,1000)
beta = 1.e+2
xt = np.linspace(0.0,4.0,20)
yt = np.sin(xt) + np.array([ np.random.normal(0.0,1.0/np.sqrt(beta)) for i in range(len(xt))])
fig = plt.figure(figsize = (15,5))
axs = [fig.add_subplot(111)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].legend()
plt.show()
plt.close()
これを,numpyモジュールの多項式fit関数と、上の計画行列によって3次式で回帰してみると…
N = len(xt)
## 多項式の次元を固定しておく
p=3
##numpyのfit
yp = np.poly1d(np.polyfit(xt, yt, p))(x)
## 計画行列を用いる方法
def phi(x,p):
return np.array([ x**i for i in range(p+1)])
Phi = np.zeros((N,p+1))
for i in range(N):
xn = xt[i]
tmp = phi(xn,p)
for j in range(p+1):
Phi[i][j] = tmp[j]
S = np.linalg.inv(np.dot(Phi.T,Phi))
wML = np.dot(S,np.dot(Phi.T,yt))
yD = [ np.dot(wML,phi(xn,p)) for xn in x ]
#図のplot
fig = plt.figure(figsize = (20,4))
axs = [fig.add_subplot(121),fig.add_subplot(122)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].plot(x,yp,label="np.polyfit",color="r",alpha=0.5)
axs[0].plot(x,yD,label="DMat",linestyle="dotted", color="g")
axs[0].legend()
axs[1].plot(x,np.log10(abs(yp-yD)))
plt.show()
plt.close()
/usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:30: RuntimeWarning: divide by zero encountered in log10
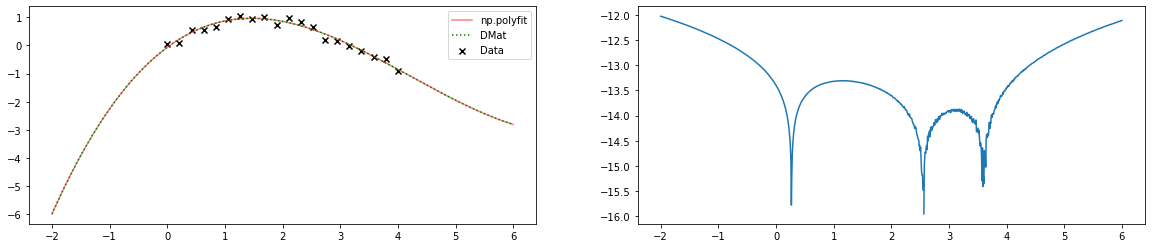
となり、ライブラリの出力と計画行列を用いた最尤推定の結果とが
ピッタリ(ざっくり14桁程度)一致していることがわかる。
マニアックな注: np.polyfitもおそらく計画行列を用いて定義されているはず。
numpyの中身を見てないので不正確かもしれませんが、
僅かな答えの差は、逆行列計算に由来するものではないかと想像します。
L2正則化項がある場合への拡張#
二乗和誤差関数に、L2正則化項を入れた場合: \(\frac{1}{2}\sum^N_{n=1} \{ t_n- {\bf w}^T \boldsymbol{\phi}({\bf x_n}) \} + \frac{\lambda}{2} {\bf w}^T{\bf w}\) に拡張してみよう。
上と同様に勾配を計算すると、最尤推定を与えるパラメータ\({\bf w}\)は
\({\bf w}_{ML,L2} = (\lambda I + \boldsymbol{\Phi}^T\boldsymbol{\Phi} )^{-1} \boldsymbol{\Phi}^T \boldsymbol{\mathrm{t}}\)
(つまり計画行列に単位行列を足すだけ)となる。
(対数尤度が\(|w|^2\)に比例することからほとんど自明だが)
あとで示すように「L2正則化を課すこと」は、パラメータのベイズ的取り扱いにおいて
「事前分布にガウス分布を仮定すること」と等価である。
ベイズ線形回帰#
次に、パラメータ\({\bf w}\)をベイズ的に取り扱う事を考える。
このノートでいう[ベイズ的]とはせいぜい「パラメータを点推定する立場より有限の幅をもつ確率分布としてパラメータを考える」という程度の意味である。
パラメータ\({\bf w}\)が、平均\(\boldsymbol{\mu}\),共分散\(\boldsymbol{\Sigma}\)で指定される多次元の正規分布に従うと仮定する: \({\bf w} \sim \mathcal{N}(\boldsymbol{\mu},\boldsymbol{\Sigma})\)
このとき、パラメータの事後分布は\(p({\bf w}|\boldsymbol{\mathcal{t}}) = \mathcal{N}(\tilde{\boldsymbol{\mu}},\tilde{\boldsymbol{\Sigma}})\)で与えられる。
ここで事後分布の平均および共分散は以下のとおりである:
\(\tilde{\boldsymbol{\Sigma}}^{-1} =\boldsymbol{\Sigma}^{-1}+\beta\boldsymbol{\Phi}^T \boldsymbol{\Phi},
\tilde{\boldsymbol{\mu}}= \tilde{\boldsymbol{\Sigma}} (\boldsymbol{\Sigma} \boldsymbol{\mu} + \beta \boldsymbol{\Phi}^T \boldsymbol{\mathcal{t}})\)
…
ここで簡単のため事前分布をさらに簡略化しよう。
事前分布の平均\(\boldsymbol{\mu}\)が\(0\)(ベクトル)かつ、
パラメータの事前分布の共分散が対角的(独立な分散をもつ)でなおかつ値が同じ,
つまり、上の\(\boldsymbol{\Sigma}=\alpha^{-1}I\)とかける場合を考える。
このとき、事後分布の平均および共分散は以下のように簡略化される:
\(\tilde{\boldsymbol{\Sigma}}^{-1} =\alpha I +\beta\boldsymbol{\Phi}^T \boldsymbol{\Phi}\)
\(\tilde{\boldsymbol{\mu}}= \beta \tilde{\boldsymbol{\Sigma}} \boldsymbol{\Phi}^T \boldsymbol{\mathcal{t}}\)
この条件のもとで対数事後確率(log posterior)は
\(\ln p({\bf w}|\boldsymbol{\mathrm{t}}) = -\frac{\beta}{2}\sum^N_{n=1} \{t_n - {\bf w}^T \phi(x_n) \}^2 -\frac{\alpha}{2} {\bf w}^T{\bf w} + \) (正規分布の係数からくるオマケの定数)となる。
したがって正規分布で与えられる事前分布のもとでパラメータ\({\bf w}\)の事後分布を最大化することは、
L2正則化項がある場合の誤差関数の最小化と(\(\lambda=\beta/\alpha\)とすれば)等価であることがわかる。
実用上は\({\bf w}\)の分布を考えたあと、それを予測値の分布として伝播させる必要がある。
一般に予測分布を評価する際は、サンプリング法などが必要になるが、”性質の良い”確率分布を用いる場合は、予測分布も閉じた形で書き下すことができる。
実際、今の場合は予測分布も正規分布になる.
未知の点\(x^*\)での値を\(t^*\)と書くことにすると、
\(p(t^*|\boldsymbol{\mathrm{t}},\alpha,\beta) = \int p(t|{\bf w},\beta) p({\bf w}|\boldsymbol{\mathrm{t}},\alpha,\beta) d{\bf w} \)
今の場合、ガウス分布の性質から、
予測分布は以下で与えられる:
\(p(t^*|{\bf x},\boldsymbol{\mathrm{t}},\alpha,\beta) = \mathcal{N}(t^*|\tilde{\boldsymbol{\mu}}^T\boldsymbol{\phi}({\bf x}),\sigma^2_N({\bf x}))\)
ここで、予測分布の分散は\(\sigma^2_N({\bf x})= \frac{1}{\beta}+\boldsymbol{\phi}({\bf x})^T \tilde{\boldsymbol{\Sigma}}\boldsymbol{\phi}({\bf x}) \)
## alpha(事前分布の精度=分散の逆数)は決め打ちとする
alpha = 1.e-5 #精度が小さい=分散が大きい=パラメータの事前知識が"弱い"
## wの事後分布の計算
I = np.diag([1.0 for i in range(p+1)])
Sigma = np.linalg.inv( alpha * I + beta * np.dot(Phi.T, Phi) )
mu = beta * np.dot(Sigma, np.dot(Phi.T,yt))
## 予測値(その分散)のリストを作成
y_BLR = []
for tx in x :
tmp = phi(tx,p)
mu_p = np.dot(mu,tmp)
term1 = 1.0/beta
term2 = np.dot(tmp,np.dot(Sigma,tmp))
sigma_p = term1 + term2
#print("term1", term1, "term2", term2)
y_BLR += [ [mu_p, sigma_p] ]
y_BLR = np.array(y_BLR).T
## plot
fig = plt.figure(figsize = (10,4))
axs = [fig.add_subplot(111)]
axs[0].scatter(xt,yt,label="Data",color="k",marker="x")
axs[0].plot(x,yD,label="Maximum Likelihood",linestyle="dotted", color="red")
axs[0].plot(x,y_BLR[0],label="Mean",linestyle="dashed", color="blue")
axs[0].fill_between(x,y_BLR[0]+np.sqrt(y_BLR[1]),y_BLR[0]-np.sqrt(y_BLR[1]),label="1sigma", color="blue",alpha=0.5)
axs[0].fill_between(x,y_BLR[0]+3*np.sqrt(y_BLR[1]),y_BLR[0]-3*np.sqrt(y_BLR[1]),label="3sigma", color="gray",alpha=0.3)
axs[0].legend()
plt.show()
plt.close()

パラメータの広がりが予測に伝搬され、
データが無いところで予測が不確かになっていることが見て取れる。
注) 上では、データの精度\(\beta\)(分散の逆数)や、パラメータ\({\bf w}\)の精度\(\alpha\)を既知とした。
実際には、\(\beta\)そのものがわからなかったりする。
(編集予定)

