常微分方程式の数値解法¶
#使用するモジュールのimport
import numpy as np
from matplotlib import pyplot as plt
常微分方程式¶
多くの自然現象や社会現象は微分方程式として定式化される。
身近な例としてはニュートンの運動方程式にはじまり、 金融や群集動態、感染症のモデルなどにも当てはまる。
このノートでは、微分方程式のうちとくに一変数関数の場合である
常微分方程式(ordinary differential equation, ODE)について
いくつかの代表的な数値解法を解説するとともに、
アルゴリズムを自分で実装してみよう。
例えば1階の常微分方程式は、一般に以下の形で書くことが出来る:
\(dx(t)/dt = f(x,t)\) (Eq. 1)
これは、ある質点の時刻\(t\)での座標を\(x(t)\)と呼ぶことにすると、
質点の位置の変化が\(f(x,t)\)の関数として書けるような状況に相当する。
注) 別に\(t\)は時間である必要はないし、
\(x(t)\)は座標以外の量(金融商品の価格など)何でも構わない。
一般に常微分方程式が与えられた時、まずはその解が変数分離などを用いて
閉じた形で書き下せないかと考えるわけだが、
実際の多くの問題ではそうは上手く行かず、数値計算が必要となる。
以下では、主として\(dx/dt = f(x,t)\)を考えるが、
高階の微分を含む場合も、
と置き換えれば、連立1階常微分方程式:
とみなすことが出来る。
常微分方程式の解を求めるためには、 適切な条件(初期条件や境界条件)を設定しなければならない。
そのうち、変数\(t\)の最初の値(初期値,初期条件)\(t_0\)と
\(x(t=t_0)\)の値が与えられた問題を初期値問題と呼ぶ。
※\(t_0\)は問題によって0だったり、\(-\infty\)だったりする。
解の存在性や下記のリプシッツ条件など適切な条件の元での
解の一意性の証明等については教科書に譲る。
###リプシッツ条件
関数\(f\)が\(U\)(たとえば\(R^n\)の部分集合) 上でリプシッツ(Lipshitz)連続であるとは、
正実数\(K\)が存在し、任意の\(x,y \in U\)に対し、
\(||f(x)-f(y)|| \leq K ||x −y||\)が成立することである。
以下では\(||\cdot||\)はユークリッドノルムとし、\(K\)をリプシッツ定数と呼ぶ。
この\(K\)が存在しているとき、
前述の常微分方程式の初期値問題は一意の解を持つ。
代表定期な数値解法¶
オイラー(Euler)法¶
1階の常微分方程式\(dx(t)/dt=f(x,y)\)を数値的に解く上で
最も基本的な考え方は時刻(便宜上そう呼ぶ)を
細かく分割した上で、\(x\)の任意時刻\(t\)での近似値を
初期値から初めて逐次的に求めていくことである。
以下では、その最も単純な例であるオイラー法を説明する。
微分の定義:
\(dx(t)/dt = \lim_{h\to 0} \frac{x(t+h) - x(t)}{h}\)から
微小変分\(h\)を十分小さく取れば、
\(x_{i+1} = x_{i} + h f(x,t_i)\)という近似式が得られる。
つまり、\(i=0\)の初期値\((x_0,t_0=0)\)から順番に上の漸化式を用いて、 \(i\)番目の時刻\(t_i\)での座標\(x_i\)を推定していく。
※一般に微小変分\(h\)は各ステップ\(i\)に依存しても良いが、簡単のため共通とした。
例: \(dx/dt = -2x^2t\), 初期条件\(x(t=0)=1.0\)のもとで
\(0 < t \leq 1.0\)での\(x\)の値を予想してみよう:
# f(x,t)のトイモデルとして dx/dt = -2tx^2 というものを考える
def f(x,t):
return - 2.0* x * x * t
#時刻tを間隔hで細かく分割する
h = 1.e-4
tr = np.arange(0.0,1.0,h)
#初期条件
x0 = 1.0
#求解
x = x0
xs = [x0]
for t in tr:
x += h * f(x,t)
xs += [x]
#描画
fig = plt.figure(figsize=(10,3))
plt.xlabel("t");plt.ylabel("x")
plt.plot(tr,xs[:-1])
plt.show()
plt.close()
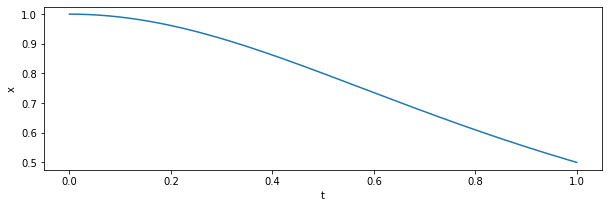
実は今の初期条件のもとでこの微分方程式は
閉じた形\(x(t)=x_0/(x_0t^2+1)\)で解が与えられるので、
真の解と数値解法による近似解を比較できる。
差分のlogを取ってみると…以下のようになる:
def fexact(t):
return x0/(x0* t*t + 1.0)
xe = np.array([ fexact(t) for t in tr])
fig = plt.figure(figsize=(10,3))
plt.xlabel("t"); plt.ylabel("abs. diff.")
plt.yscale("log")
plt.plot(tr,abs(xe-np.array(xs[:-1])))
plt.show()
plt.close()
Taylor展開するだけで簡単に調べられるようにEuler法は局所打ち切り誤差が\(O(h^2)\)、
大局打切り誤差が\(\sim O(h^2)\times O(h^{-1})\sim O(h)\)の手法となっている。
つまり1桁精度を上げたいなら\(h\)を1/10、つまり計算量を10倍にしなくてはならない。
上の\(h\)を変えてチェックしてみよう。
大局誤差が\(h\)の\(p\)乗に比例する手法を一般に\(p\)次公式と呼び
上のEuler法は1次公式となる。
Euler法に少し工夫を加えた修正Euler法は、2次公式であり
\(h\)を1/10すると、大局誤差は1/100にできる。
4次のルンゲクッタ法 (RK4)¶
次に4次公式の代表例である4次のルンゲクッタ法を紹介しよう。
古典的ルンゲ=クッタ法などとも呼ばれるこの方法は、
幾つかの\((x,t)\)に対して\(f(x,t)\)の値を計算し、
打切り誤差が互いにキャンセルしあうように
うまく重み付けをして次ステップの\(x\)の値を求めていく方法であり
様々なところで用いられている。
基本的には2変数関数のTaylor展開をやれば更新式を導出できるが 煩雑なので導出については省略することにして結果だけ示すと
\(i\)番目のステップでの\(x,t\)の値\(x_i,t_i\)が所与のとき、
以下の4点での\(f(x,t)\)の(近似)値を用意して
\( f_1 = f(x_i,t_i),
f_2 = f(x_i+\frac{h}{2} f_1,t_i+\frac{h}{2}),\)
\(f_3 = f(x_i+\frac{h}{2} f_2,t_i+\frac{h}{2}),
f_4 = f(x_i+h f_3,t_i+h)
\)
\(x_{i+1} = x_{i} + \frac{h}{6} (f_1+2f_2+2f_3 + f_4 )\) とすることで、4次公式が得られる。
また、前述のような”重み付け”の選択には自由度があり、
\( f_1 = f(x_i,t_i),
f_2 = f(x_i+\frac{h}{3} f_1,t_i+\frac{h}{3}),\)
\(
f_3 = f(x_i-\frac{h}{3}f_1 + h f_2,t_i+\frac{2h}{3}),
f_4 = f(x_i+hf_1-hf_2+h f_3,t_i+h)
\)
\(x_{i+1} = x_{i} + \frac{h}{8} (f_1+3f_2+3f_3 + f_4 )\)
という公式も知られている。
前者を実装して、先程の例でEuler法と比べてみると…
#求解(RK4)
xsRK4 = [x0]
x = x0
for t in tr:
f1 = f(x,t)
f2 = f(x+0.5*h*f1, t+0.5*h)
f3 = f(x+0.5*h*f2, t+0.5*h)
f4 = f(x+h*f3, t+h)
x += h*(f1 + 2*f2 + 2*f3 + f4)/6.0
xsRK4 += [x]
#描画
fig = plt.figure(figsize=(10,3))
plt.xlabel("t");plt.ylabel("abs. diff.")
plt.yscale("log")
plt.plot(tr,abs(xe-np.array(xs[:-1])),label="Euler")
plt.plot(tr,abs(xe-np.array(xsRK4[:-1])),label="RK4")
plt.legend()
plt.show()
plt.close()
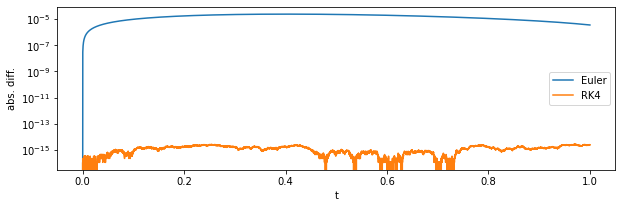
となり、高精度で解が得られていることが分かる。
積分を用いた解法¶
常微分方程式 \(\frac{dx}{dt} = f(x,t)\)は形式的には
\(x(t') = x(t_0) + \int^{t'}_{t_0} f(x(t),t,) dt\) と書くことが出来る。
右辺の積分を数値的に計算することで、
元の微分方程式の解を求めることを考えよう。
Adams-Bashforth法¶
以下では特に、Adams-Bashforth法(AB法)と呼ばれる手法を考える。
まずは、2次のAB法を考えよう。
\(t_i\)と\(t_{i+1}\)の間の\(f(x(t),t)\)を、現在居る\(i\)番目のステップと
1個前の\(i-1\)番目のステップを用いて、1次のLagrange補間で近似してみる。
\( \begin{align} x_{i+1} &= x_i + \int^{t_{i+1}}_{t_i} P_1(t) dt \\ P_1(t) &= f_{i-1}L_{i-1}(t) + f_i L_i(t) \\ L_{i-1} &= \frac{t-t_i}{t_{i-1}-t_i}, L_{i} = \frac{t-t_{i-1}}{t_{i}-t_{i-1}} \end{align}\)
各ステップの刻み幅\(t_{i}-t_{i-1}\) for \(\forall i \)を一定\(h\)としよう。
このもとで上の積分を評価すると、
\(x_{i+1} = x_i + \frac{h}{2} (-f_{i-1}+3f_i)\)
という更新式を得る。
この手法の局所打切り誤差は(またTaylor展開して)\(O(h^3)\)であり、
２次の公式となる。一般的な分類に倣えば、この手法は過去の2ステップの情報を利用する、
陽(explicit)解法かつ２段法(2-step method)となっている。
同様にして、一般に\(m\)ステップのAB法(\(n-1\)次のLegendre補間を使用)は\(m\)次公式を与える。
たとえば4次公式は\(x_{i+1}=x_i + \frac{h}{24}(-9f_{i-3} + 37f_{i-2} -59f_{i-1} +55f_{i})\)
Adams-Bashforth法とRunge-Kutta法の違い
AB法では、過去に評価した\(f\)の値を用いるため、計算量の増加を防ぐことができる。
つまり、各\(f\)の評価は１回だけで良い。
一方で、RK4では各ステップで\(f\)を４回計算する必要がある。
これは\(f\)の評価が複雑な場合
(例えば解きたい微分方程式が行列(連立)になっていて、\(f\)に行列演算を含む場合など)
Runge-Kutta法よりも、高速に計算できるかもしれない。
一方で、\(m\)次のAB法では過去の情報を利用するため、
はじめの\(m-1\)回については、RK法などで予め求めておく必要がある。
また、Runge-Kutta法と比較すると、誤差が大きかったり、
数値的に不安定になりやすいことも知られている。
def AB4(x0,m=4):
xsAB = [x0]
x = x0
fs = [ 0.0 for i in range(m)]
for i,t in enumerate(tr):
if len(xsAB) < m : #RK4
f1 = f(x,t)
f2 = f(x+0.5*h*f1, t+0.5*h)
f3 = f(x+0.5*h*f2, t+0.5*h)
f4 = f(x+h*f3, t+h)
x += h*(f1 + 2*f2+ 2*f3 + f4)/6.0
fs[0] = f1; fs[1] = f2; fs[2] = f3; fs[3] = f4
else:
f1,f2,f3 = fs[1:]
f4 = f(x,t)
x += h *(-9*f1 +37*f2 -59*f3 +55*f4 )/24.0
fs[0] = f1; fs[1] = f2; fs[2] = f3; fs[3] = f4
xsAB += [x]
return xsAB
xsAB4 = AB4(x0)
#描画
fig = plt.figure(figsize=(10,3))
plt.xlabel("t");plt.ylabel("abs. diff.")
plt.yscale("log")
plt.plot(tr,abs(xe-np.array(xs[:-1])),label="Euler")
plt.plot(tr,abs(xe-np.array(xsRK4[:-1])),label="RK4")
plt.plot(tr,abs(xe-np.array(xsAB4[:-1])),label="AB4")
plt.legend()
plt.show()
plt.close()
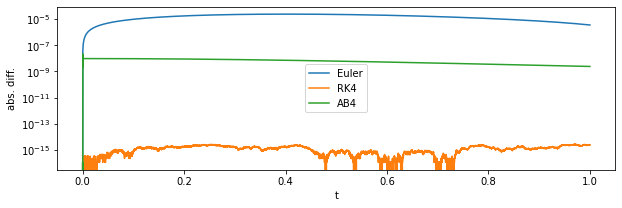
Adams-Moulton法¶
AB法は、現在\(i\)と過去のステップの情報のみを使用したが、
\(i+1\)ステップの情報を使う(陰解法)ことで、より高精度の結果を得ることができる。
3次のAB法(\(i-2,i-1,i\)の情報)に加えて\(i+1\)番目の情報を用いて
3次のLagrange補間多項式\(P_3(t)=\sum^2_{j=-1}f_{i-j}L_{i-j}\)のもと
\(x_{i+1}=x_i + \sum^2_{j=-2} f_{i+j} \int^{t_{i+1}}_{t_i} L_{i+j}(t) dt \)
という
更新式を考える。愚直に上と同様に各積分を評価すると
\(x_{i+1}=x_i + \frac{h}{24}(f_{i-2}-5f_{i-1}+19f_{i} +9f_{i+1}) \)
という式が得られる。
これは、４次精度の公式になっており、3ステップ(4次)のAdams-Moulton法と呼ばれる。
右辺にある\(f_{i+1}\)の評価に関する計算コストの分だけ、3次のAB法に比べて増えることになる。
Adams-Bashforth-Moulton法¶
AM法とAB法を組み合わせることで、使いやすい高精度な陽解法を作ろう
というのが予測子修正子法の発想である。
4ステップのAB法を予測子, 4ステップのAM法を修正子として採用すると
以下の更新式が得られる:
\(\begin{align} x^{P}_{i+1} &= x_i + \frac{h}{24}(-9f_{i-3}+37f_{i-2}-59f_{i-1}+55f_i) \\ x_{i+1} &= x_i + \frac{h}{24}(f_{i-2}-5f_{i-1}+19f_i + 9f(t_{i+1},x^P_{i+1})) \end{align} \)
def ABM(x0,m=4):
xsABM = [x0]
x = x0
fs = [ 0.0 for i in range(m)]
for i,t in enumerate(tr):
if len(xsABM) < m : #RK4
f1 = f(x,t)
f2 = f(x+0.5*h*f1, t+0.5*h)
f3 = f(x+0.5*h*f2, t+0.5*h)
f4 = f(x+h*f3, t+h)
x += h*(f1 + 2*f2+ 2*f3 + f4)/6.0
fs[0] = f1; fs[1] = f2; fs[2] = f3; fs[3] = f4
else:
f1,f2,f3 = fs[1:]; f4 = f(x,t)
## 予測子
xp = x + h *(-9*f1+37*f2-59*f3+55*f4) / 24.0
f5 = f(xp,t+h)
## 修正子
x += h *(f2 -5*f3 +19*f4 +9*f5 )/24.0
fs[0] = f1; fs[1] = f2; fs[2] = f3; fs[3] = f4
xsABM += [x]
return xsABM
xsABM = ABM(x0)
fig = plt.figure(figsize=(10,3))
plt.xlabel("t");plt.ylabel("abs. diff.");plt.yscale("log")
plt.plot(tr,abs(xe-np.array(xs[:-1])),label="Euler")
plt.plot(tr,abs(xe-np.array(xsRK4[:-1])),label="RK4")
plt.plot(tr,abs(xe-np.array(xsAB4[:-1])),label="AB4")
plt.plot(tr,abs(xe-xsABM[:-1]),label="ABM4")
plt.legend();plt.show();plt.close()
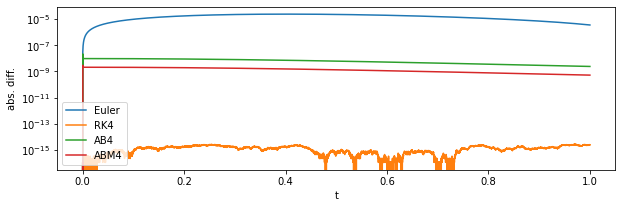
1桁程度、AB法よりも精度が改善していることがわかる。